题目内容
已知平面直角坐标系xOy中,A(4+2| 3 |
(1)求圆C的方程;
(2)若过点(2,6)的直线l被圆C所截得的弦长为4
| 3 |
分析:(1)由题意设出圆的一般式方程,把三点坐标代入列方程组,求出系数;
(2)分两种情况求解:当直线的斜率不存在时,只需要验证即可;当直线的斜率存在时,根据弦的一半、半径和弦心距构成直角三角形来求直线的斜率.
(2)分两种情况求解:当直线的斜率不存在时,只需要验证即可;当直线的斜率存在时,根据弦的一半、半径和弦心距构成直角三角形来求直线的斜率.
解答:解:(1)设圆C方程为x2+y2+Dx+Ey+F=0,由题意列方程组,
解得D=-8,E=F=0.
∴圆C:(x-4)2+y2=16.
(2)当斜率不存在时,l:x=2被圆截得弦长为4
,符合题意;
当斜率存在时,设直线l:y-6=k(x-2),
即kx-y+6-2k=0,
∵被圆截得弦长为4
,
∴圆心到直线距离为2,
∴
=2,解得k=-
,
∴直线l:y-6=-
(x-2),即4x+3y-26=0.
故所求直线l为x=2,或4x+3y-26=0.
|
解得D=-8,E=F=0.
∴圆C:(x-4)2+y2=16.
(2)当斜率不存在时,l:x=2被圆截得弦长为4
| 3 |
当斜率存在时,设直线l:y-6=k(x-2),
即kx-y+6-2k=0,
∵被圆截得弦长为4
| 3 |
∴圆心到直线距离为2,
∴
| |4k+6-2k| | ||
|
| 4 |
| 3 |
∴直线l:y-6=-
| 4 |
| 3 |
故所求直线l为x=2,或4x+3y-26=0.
点评:本题考查了用待定系数法求圆的方程,通常用一般式计算要简单;另外圆与直线相交时,半径、弦长的一半和弦心距的关系,注意用到斜率考虑是否存在问题,这是易错出.

练习册系列答案
相关题目
 已知平面直角坐标系xOy上的区域D由不等式组
已知平面直角坐标系xOy上的区域D由不等式组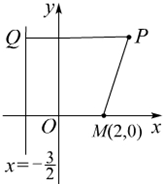 已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x=
已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x=