题目内容
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)若对任意的![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据“零点分段法”分为![]() 、
、![]() 、
、![]() 三种情形,分别解出不等式,再取并集即可;(2)将
三种情形,分别解出不等式,再取并集即可;(2)将![]() 用分段函数进行表示,令
用分段函数进行表示,令![]() ,原题意等价于函数
,原题意等价于函数![]() 的图象在直线
的图象在直线![]() 的下方或在直线
的下方或在直线![]() 上,结合图可得结果.
上,结合图可得结果.
试题解析:(1)当![]() 时,不等式转化为
时,不等式转化为![]() ,解得
,解得![]() ;
;
当![]() 时,不等式转化为
时,不等式转化为![]() ,解得
,解得![]() ;
;
当![]() 时,不等式转化为
时,不等式转化为![]() ,解得
,解得![]() .
.
综上所述,不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(2)由(1)得,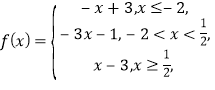
作出其函数图象如图所示:
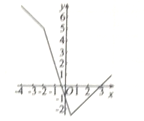
令![]() ,若对任意的
,若对任意的![]() ,都有
,都有![]() 成立,
成立,
即函数![]() 的图象在直线
的图象在直线![]() 的下方或在直线
的下方或在直线![]() 上.
上.
当![]() 时,
时,![]() ,无解;
,无解;
当![]() 时,
时,![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() .
.
综上可知,当![]() 时满足条件,故实数
时满足条件,故实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目




