题目内容
如图，在梯形ABCD中，AB∥CD，∠ADC＝90°，3AD＝DC＝3，AB＝2，E是DC上一点，满足DE＝1，连接AE，将△DAE沿AE折起到△D1AE的位置，使得∠D1AB＝60°，设AC与BE的交点O．
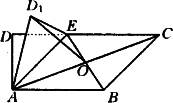
(1)判断平面D1AE与平面ABCE是否垂直？并说明理由．
(2)求异面直线OD1与AE所成角的余弦值；
答案：
解析：
解析：
|
解：(1)设AE的中点为M，则 而D1M 所以，平面AD1E⊥平面ABCE (2)在Rt△ADE中，AE＝
所以， |
平面AD1E，
，又AD1＝AD＝1，∠EAD1＝∠EAD＝450，
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
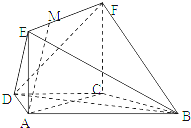如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，．∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上．
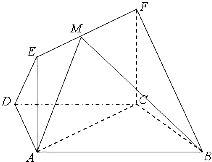如图，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，CF=1．
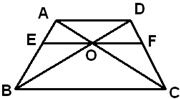如图，在梯形ABCD中，AD∥BC，BD与AC相交于O，过O的直线分别交AB、CD于E、F，且EF∥BC，若AD=12，BC=20，则EF=
如图，在梯形ABCD中，对角线AC和BD交于点O，E、F分别是AC和BD的中点，分别写出
如图，在梯形△ABCD中，AB∥CD，AD=DC-=CB=1，么ABC-60．，四边形ACFE为矩形，平面ACFE上平面ABCD，CF=1．