题目内容
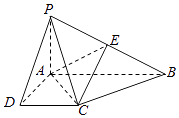
【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AD⊥AB，DC∥AB，PA=1，AB=2，PD=BC= 
． 
（1）求证：平面PAD⊥平面PCD；
（2）试在棱PB上确定一点E，使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2：1；
（3）在（2）的条件下，求二面角E﹣AC﹣P的余弦值．
【答案】
（1）证明：∵AD⊥AB，DC∥AB，∴DC⊥AD，
∵PA⊥平面ABCD，DC平面ABCD，∴DC⊥PA，
∵AD∩PA=A，∴DC⊥平面PAD，
∵DC平面PCD，
∴平面PAD⊥平面PCD
（2）解：作EF⊥AB于F点，
在△ABP中，PA⊥AB，∴EF∥PA，
∴EF⊥平面ABCD，
设EF=h，AD= 
=1， 
，
则 
，
= 
= 
，
由VPDCEA：VEACB=2：1，得（ 
）： 
=2：1，解得h= ，
EF= PA，故E为PB的中点
（3）解：连结FC，FD，FD与AC交于点O，连结OE，
由（2）知EF⊥平面ABCD，∴EF⊥AC，
∵ADCF为正方形，∴FO⊥AC，
∵FO∩EF=F，
∴AC⊥平面EFO，∴EO⊥AC，
∴∠EOF是二面角E﹣AC﹣B的平面角，
∵PA⊥平面ABCD，∴平面PAC⊥平面ABCD，
∴二面角E﹣ACB与二面角E﹣AC﹣P互余，
设二面角E﹣AC﹣P的平面角为θ，
则cosθ=sin∠EOF，
在Rt△EOF中，EF= ，FO= 
，EO= 
，
cosθ=sin 
，
∴二面角E﹣AC﹣P的余弦值为 
【解析】（1）推导出DC⊥AD，DC⊥PA，由此能证明平面PAD⊥平面PCD．（2）作EF⊥AB于F点，则EF⊥平面ABCD，设EF=h，由VPDCEA：VEACB=2：1，解得h= ，从而得到E为PB的中点．（3）连结FC，FD，FD与AC交于点O，连结OE，推导出EF⊥AC，FO⊥AC，EO⊥AC，从而∠EOF是二面角E﹣AC﹣B的平面角，由二面角E﹣ACB与二面角E﹣AC﹣P互余，能求出二面角E﹣AC﹣P的余弦值．
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识，掌握一个平面过另一个平面的垂线，则这两个平面垂直．
