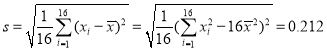Question

【题目】若一个四棱锥底面为正方形，顶点在底面的射影为正方形的中心，且该四棱锥的体积为9，当其外接球表面积最小时，它的高为（ ）
A.3
B.2
C.2
D.3

Answer 1

【答案】A
【解析】解：设底面边长AB=a，棱锥的高SM=h， ∵V棱锥S﹣ABCD= a2h=9，
∴a2= ，
∵正四棱锥内接于球O，
∴O在直线SM上，设球O半径为R，
（i）若O在线段SM上，如图一，则OM=SM﹣SO=h﹣R，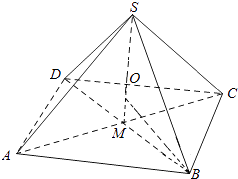

（ii）若O在在线段SM的延长线上，如图二，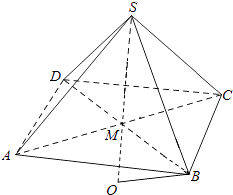

则OM=SO﹣SM=R﹣h，
∵SM⊥平面ABCD，
∴△OMB是直角三角形，
∴OM2+MB2=OB2 ，
∵OB=R，MB= BD= a，
∴（h﹣R）2+ =R2 ， 或（R﹣h）2+ =R2
∴2hR=h2+ ，
即R= + = + = ≥3 = ．
当且仅当 = 取等号，
即h=3时R取得最小值 ．
故选：A．
【考点精析】关于本题考查的棱锥的结构特征，需要了解侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方才能得出正确答案．