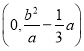题目内容
【题目】某公司为了获得更大的收益,每年要投入一定的资金用于广告促销,经调查,每年投入广告费t百万元,可增加销售额约为![]() 百万元.
百万元.
(Ⅰ)若该公司将一年的广告费控制在4百万元之内,则应投入多少广告费,才能使该公司由此增加的收益最大?
(Ⅱ)现该公司准备共投入5百万元,分别用于广告促销和技术改造,经预测,每投入技术改造费![]() 百万元,可增加的销售额约为
百万元,可增加的销售额约为![]() 百万元,请设计一个资金分配方案,使该公司由此增加的收益最大.
百万元,请设计一个资金分配方案,使该公司由此增加的收益最大.
(注:收益=销售额-投入,这里除了广告费和技术改造费,不考虑其他的投入)
【答案】(1)投入3百万元的广告费时,该公司由此增加的收益最大.(2)4百万元用于技术改造,1百万元用于广告促销,该公司由此增加的收益最大
【解析】分析:(Ⅰ)先写出收益f(t)的解析式,再利用二次函数的图像和性质求最大值和此时t 的值. (Ⅱ)设由此增加的收益是g(x)百万元,再写出g(x)的解析式,再利用导数求函数的最值,即得资金分配方案.
详解:(Ⅰ)设投入t百万元的广告费后增加的收益为f(t)百万元,
则由![]() ,
,
∴当t=3时,f(t)取得最大值9,即投入3百万元的广告费时,该公司由此增加的收益最大.
(Ⅱ)用于技术改造的资金为x百万元,则用于广告促销的资金为(5-x)百万元,设由此增加的收益是g(x)百万元.
则![]() .
.
![]() .
.
则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴当x=4时,g(x)取得最大值.
即4百万元用于技术改造,1百万元用于广告促销,该公司由此增加的收益最大.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】某校高二理科1班共有50名学生参加学业水平模拟考试,成绩(单位:分,满分100分)大于或等于90分的为优秀,其中语文成绩近似服从正态分布![]() ,数学成绩的频率分布直方图如图.
,数学成绩的频率分布直方图如图.
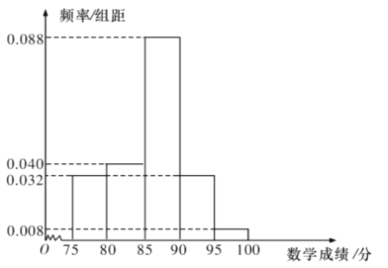
(1)这50名学生中本次考试语文、数学成绩优秀的大约各有多少人?
(2)如果语文和数学两科成绩都优秀的共有4人,从语文优秀或数学优秀的这些同学中随机抽取3人,设3人中两科都优秀的有X人,求X的分布列和数学期望;
(3)根据(1)(2)的数据,是否有99%以上的把握认为语文成绩优秀的同学,数学成绩也优秀?
语文优秀 | 语文不优秀 | 合计 | |
数学优秀 | |||
数学不优秀 | |||
合计 |
附:①若![]() ,则
,则![]() ,
,![]() ;②
;②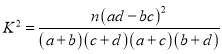 ;
;
③
| 0.1 | 0.05 | 0.025 | 0.010 | p>0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |