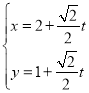题目内容
【题目】设命题![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,命题
,命题![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() :
:![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
【答案】(1)![]() 或
或![]() ;(2)1.
;(2)1.
【解析】
(1)由对数的运算、导函数的应用,可得![]() :
:![]() ,
,![]() :
:![]() ,再结合复合命题的真假即可得解;
,再结合复合命题的真假即可得解;
(2)由![]() 是
是![]() 的必要不充分条件,结合(1)可得
的必要不充分条件,结合(1)可得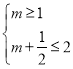 ,求解即可.
,求解即可.
解:(1)因为![]() ,
,
因为![]() ,所以
,所以![]() ,解得得
,解得得![]() ,即
,即![]() :
:![]() .
.
又因为![]() ,∵函数
,∵函数![]() 无极值点,∴
无极值点,∴![]() 恒成立,则
恒成立,则![]() ,解得
,解得![]() ,即
,即![]() :
:![]() .
.
∵“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,∴
”为真命题,∴![]() 与
与![]() 只有一个命题是真命题.
只有一个命题是真命题.
若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() ,
,![]() .
.
若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
(2)∵“![]() ”为真命题,∴
”为真命题,∴![]() .
.
又![]() ,∴
,∴![]() 或
或![]() , 从而
, 从而![]() :
:![]() .
.
∵![]() 是
是![]() 的必要不充分条件,即
的必要不充分条件,即![]() 是
是![]() 的充分不必要条件,
的充分不必要条件,
∴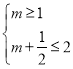 ,解得
,解得![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
故正整数![]() 的值为
的值为![]() .
.

练习册系列答案
相关题目