题目内容
(2010•潍坊三模)设数列{an}的前n项和为Sn,对一切n∈N,Sn=n2+
an.
(1)求数列{an}的通项公式;
(2)令bn=λqan+λ(λ,q为常数,q>0且q≠1),cn=(b1+b2+…+bn)+n+3,当数列{cn}为等比数列时,求实数对(λ,q)的值;
(3)若不等式(1-
)(1-
)…(1-
)
<a-
对一切n∈N*都成立,求a的取值范围.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)令bn=λqan+λ(λ,q为常数,q>0且q≠1),cn=(b1+b2+…+bn)+n+3,当数列{cn}为等比数列时,求实数对(λ,q)的值;
(3)若不等式(1-
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| an+1 |
| 3 |
| 2a |
分析:(1)由题意令n=1,得a1=1+
a1,a1=2.令n=2,得a1+a2=4+
a2,a2=4.令n=3,得a1+a2 +a3=9+
a3,a3=6.由此猜想:an=2n.然后再用数学归纳法证明.
(2)由bn=λq2n+λ,知Cn=λn+
+n+3=3+
-
+(λ+1)n,由此知cn=3•(
)n为等比数列,从而求出实数对(λ,q)的值.
(3)设g(n)=(1-
)(1-
)…(1-
)•
,由于
=(1-
)•
=
<1.所以g(n+1)<g(n),由此能够求出a的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由bn=λq2n+λ,知Cn=λn+
| λq2(1-q2n) |
| 1-q2 |
| λq2 |
| 1-q2 |
| λq2n+2 |
| 1-q2 |
| 3 |
| 4 |
(3)设g(n)=(1-
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 2n+1 |
| g(n+1) |
| g(n) |
| 1 |
| an+1 |
| ||
|
| ||
|
解答:解:(1)由题意Sn=n2+
an.
令n=1,得a1=1+
a1,
∴a1=2.
令n=2,得a1+a2=4+
a2,∴a2=4.
令n=3,得a1+a2 +a3=9+
a3,∴a3=6.
由此猜想:an=2n.
由数学归纳法证明如下:
①当n=1时,由上面的求解知a1=2,猜想成立.
②假设n=k(k≥1,k∈N*)时,猜想成立,
则当n=k+1时,注意到Sn=n2+
an,n∈N*,
故Sk+1=(k+1)2+
ak+1,
Sk=n2+
an(n∈N*),
故Sk+1=(k+1)2+
ak+1,
Sk=k2+
ak,
两式相减,得ak+1=2k+1+
ak+1-
ak,
∴ak+1=4k+2-ak,
由假设ak=2k,
故ak+1=4k+2-ak=4k+2-2k=2(k+1),
∴n=k+1时,猜想也成立.
由①②知,对一切n∈N*,an=2n成立.
(2)依题意,bn=λq2n+λ,
∴Cn=λn+
+n+3
=3+
-
+(λ+1)n,
令
,
.
此时,cn=3•(
)n为等比数列,
故所求的实数对为(-1,±
).
(3)设g(n)=(1-
)(1-
)…(1-
)•
,
由于
=(1-
)•
=
<1.
所以g(n+1)<g(n),
故g(n)max=g(1)=
.
令
<a-
,
即
> 0,
解得-
<a<0,或a>
.
| 1 |
| 2 |
令n=1,得a1=1+
| 1 |
| 2 |
∴a1=2.
令n=2,得a1+a2=4+
| 1 |
| 2 |
令n=3,得a1+a2 +a3=9+
| 1 |
| 2 |
由此猜想:an=2n.
由数学归纳法证明如下:
①当n=1时,由上面的求解知a1=2,猜想成立.
②假设n=k(k≥1,k∈N*)时,猜想成立,
则当n=k+1时,注意到Sn=n2+
| 1 |
| 2 |
故Sk+1=(k+1)2+
| 1 |
| 2 |
Sk=n2+
| 1 |
| 2 |
故Sk+1=(k+1)2+
| 1 |
| 2 |
Sk=k2+
| 1 |
| 2 |
两式相减,得ak+1=2k+1+
| 1 |
| 2 |
| 1 |
| 2 |
∴ak+1=4k+2-ak,
由假设ak=2k,
故ak+1=4k+2-ak=4k+2-2k=2(k+1),
∴n=k+1时,猜想也成立.
由①②知,对一切n∈N*,an=2n成立.
(2)依题意,bn=λq2n+λ,
∴Cn=λn+
| λq2(1-q2n) |
| 1-q2 |
=3+
| λq2 |
| 1-q2 |
| λq2n+2 |
| 1-q2 |
令
|
|
此时,cn=3•(
| 3 |
| 4 |
故所求的实数对为(-1,±
| ||
| 2 |
(3)设g(n)=(1-
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 2n+1 |
由于
| g(n+1) |
| g(n) |
| 1 |
| an+1 |
| ||
|
=
| ||
|
所以g(n+1)<g(n),
故g(n)max=g(1)=
| ||
| 2 |
令
| ||
| 2 |
| 3 |
| 2a |
即
(a-
| ||||
| a |
解得-
| ||
| 2 |
| 3 |
点评:本题考查数列与不等式的综合应用,综合性强,难度较大,容易出错.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
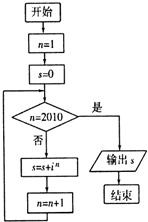 (2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )
(2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )