题目内容
在平面直角坐标系xOy中，设A、B、C是圆x2+y2=1上相异三点，若存在正实数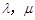
，使得
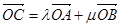，则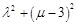
的取值范围是 ．
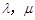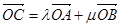，使得，则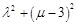的取值范围是 ．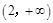
试题分析：∵∵A，B，C互异，∴-1＜
＜1，由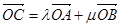得μ2=1+λ2-2λ，则f（λ）=（λ-3）2+μ2=2λ2-6λ-2λ2+10＞2λ2-8λ+10≥2．又f（λ）=（λ-3）2+μ2=2λ2-6λ-2λ2+10＜2λ2-4λ+10，无最大值，∴（λ-3）2+μ2的取值范围是（2，+∞）．点评：本题考查向量知识的运用，考查函数的最值，确定函数解析式是关键．
练习册系列答案
阅读快车系列答案
相关题目
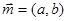，向量
，向量p＝(b－2，a－2)
∥
，求证△ABC为等腰三角形；
，边长c＝2，
, 求 △ABC的面积．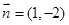
的直线（点法式）方程为
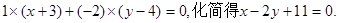类比以上方法，在空间直角坐标系中，经过点A（1，2，3）且法向量为
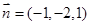的平面（点法式）方程为 。（请写出化简后的结果）
，向量
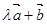与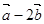
垂直，则实数
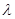的值为( ).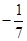
与
的夹角为
，
，
，则
与
不共线，
，且
，则向量
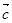的夹角为
ABC中,M是BC的中点,AM ="3,BC" =10,则
=______________
，
且（
）⊥
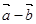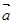，则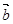
的夹角是 （ ）
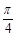
中，满足
,
是
中点.
,求向量
与向量
的夹角的余弦值；
是线段
上任意一点，且
，求
的最小值；
是
,
，
,求
的最小值.