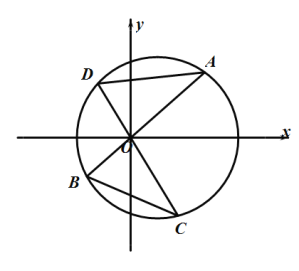
题目内容
【题目】设椭圆![]() ,定义椭圆C的“相关圆”E为:
,定义椭圆C的“相关圆”E为:![]() .若抛物线
.若抛物线![]() 的焦点与椭圆C的右焦点重合,且椭圆C的短轴长与焦距相等.
的焦点与椭圆C的右焦点重合,且椭圆C的短轴长与焦距相等.
(1)求椭圆C及其“相关圆”E的方程;
(2)过“相关圆”E上任意一点P作其切线l,若l 与椭圆![]() 交于A,B两点,求证:
交于A,B两点,求证:![]() 为定值(
为定值(![]() 为坐标原点);
为坐标原点);
(3)在(2)的条件下,求![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() ,
,![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)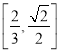 .
.
【解析】
(1)由题设知![]() ,又
,又![]() ,从而可得
,从而可得![]() ,得椭圆方程,及相关圆方程;
,得椭圆方程,及相关圆方程;
(2)对直线![]() 斜率进行讨论,斜率不存在时,直接写出直线
斜率进行讨论,斜率不存在时,直接写出直线![]() 方程,求出
方程,求出![]() 坐标,得
坐标,得![]() ,
,
斜率存在时,设直线![]() 方程为
方程为![]() ,与椭圆方程联立方程组,消元后得关于
,与椭圆方程联立方程组,消元后得关于![]() 的二次方程,有韦达定理得
的二次方程,有韦达定理得![]() ,由直线与圆相切得
,由直线与圆相切得![]() 关系,计算
关系,计算![]() 也可得
也可得![]() ,定值.
,定值.
(3)由于![]() 是“相关圆”半径,所以
是“相关圆”半径,所以![]() ,结合韦达定理求得
,结合韦达定理求得![]() ,并得到其范围,从而得面积的范围.
,并得到其范围,从而得面积的范围.
(1)抛物线![]() 的焦点是
的焦点是![]() ,与椭圆的一个焦点重合,∴
,与椭圆的一个焦点重合,∴![]() ,又
,又![]() ,所以
,所以![]() ,
,
椭圆方程为![]() ,“相关圆”
,“相关圆”![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 斜率不存在时,不妨设其方程为
斜率不存在时,不妨设其方程为![]() ,则
,则![]() ,可得
,可得![]() .
.
当直线![]() 斜率存在时,设其方程为
斜率存在时,设其方程为![]() ,设
,设![]() ,由
,由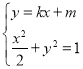 得
得![]() ,
,
![]() ,即
,即![]() ,
,
由韦达定理得![]() ,
,![]() .
.
因为直线![]() 与圆相切,所以
与圆相切,所以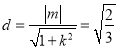 ,整理得
,整理得![]() ,
,
所以![]()
![]()
![]() ,所以
,所以![]() ,
,![]() ,为定值.
,为定值.
(3)由于![]() ,因此求
,因此求![]() 面积的取值范围只要求弦长
面积的取值范围只要求弦长![]() 的取值范围.
的取值范围.
当直线![]() 斜率不存在时,
斜率不存在时,![]() ,
,![]() ,
,
当直线![]() 斜率存在时,
斜率存在时,
![]()
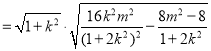
![]()
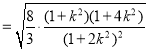
![]() ,
,
![]() 时,
时,![]() 0,
0,
![]() 时,
时,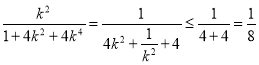 ,
,
∴![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 即
即![]() 时,
时,![]() .
.
所以![]() 的取值范围是
的取值范围是![]() ,
,
故![]() 面积的取值范围是
面积的取值范围是![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目