题目内容
已知数列{an}满足, .
.(1)若方程f(x)=x的解称为函数y=f(x)的不动点,求an+1=f(an)的不动点的值;
(2)若a1=2,
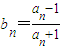 ,求证:数列{lnbn}是等比数列,并求数列{bn}的通项.
,求证:数列{lnbn}是等比数列,并求数列{bn}的通项.(3)当任意n∈N*时,求证:b1+b2+b3+…+bn<
 .
.
【答案】分析:(1)根据方程不动点的定义,令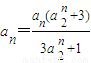 ,解得an的值,
,解得an的值,
(2)把等式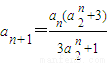 两边同时加1和两边同时减1,得到两式相除得
两边同时加1和两边同时减1,得到两式相除得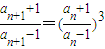 ,据此可以得数列lnbn是以-ln3为首项,3为公比的等比数列,于是可以数列{bn}的通项,
,据此可以得数列lnbn是以-ln3为首项,3为公比的等比数列,于是可以数列{bn}的通项,
(3)根据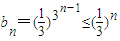 ,求得数列{
,求得数列{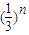 }前n项和,然后判断其和与
}前n项和,然后判断其和与 的大小.
的大小.
解答:解:(1)由方程an+1=f(an)得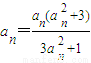 ,
,
解得an=0,或an=-1,或an=1.
(2)∵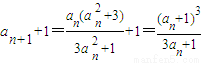 ,
,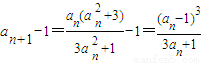 ,
,
∴两式相除得 ,
,
即bn+1=bn3.
由a1=2可以得到bn>0,则lnbn+1=lnbn3=3lnbn.
又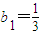 ,得lnb1=-ln3,
,得lnb1=-ln3,
∴数列lnbn是以-ln3为首项,3为公比的等比数列.
∴ ,
,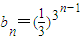 (n∈N*).
(n∈N*).
(3)任意n∈N*,3n-1≥n.∴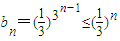 ,
,
∴b1+b2+b3++bn<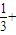
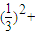
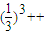
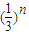
=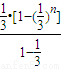 <
< .
.
点评:本题主要考查数列求和和求等比数列的通项公式的知识点,解答本题的关键是熟练掌握等比数列的性质,还需掌握运用放缩法解答不等式,本题是一道综合性试题,难度一般.
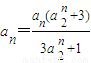 ,解得an的值,
,解得an的值,(2)把等式
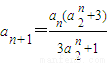 两边同时加1和两边同时减1,得到两式相除得
两边同时加1和两边同时减1,得到两式相除得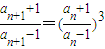 ,据此可以得数列lnbn是以-ln3为首项,3为公比的等比数列,于是可以数列{bn}的通项,
,据此可以得数列lnbn是以-ln3为首项,3为公比的等比数列,于是可以数列{bn}的通项,(3)根据
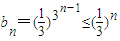 ,求得数列{
,求得数列{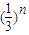 }前n项和,然后判断其和与
}前n项和,然后判断其和与 的大小.
的大小.解答:解:(1)由方程an+1=f(an)得
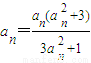 ,
,解得an=0,或an=-1,或an=1.
(2)∵
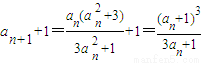 ,
,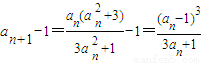 ,
,∴两式相除得
 ,
,即bn+1=bn3.
由a1=2可以得到bn>0,则lnbn+1=lnbn3=3lnbn.
又
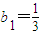 ,得lnb1=-ln3,
,得lnb1=-ln3,∴数列lnbn是以-ln3为首项,3为公比的等比数列.
∴
 ,
,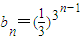 (n∈N*).
(n∈N*).(3)任意n∈N*,3n-1≥n.∴
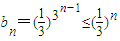 ,
,∴b1+b2+b3++bn<
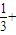
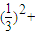
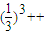
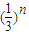
=
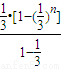 <
< .
.点评:本题主要考查数列求和和求等比数列的通项公式的知识点,解答本题的关键是熟练掌握等比数列的性质,还需掌握运用放缩法解答不等式,本题是一道综合性试题,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目