题目内容
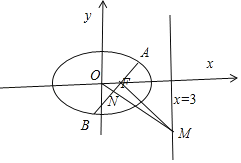
【题目】已知椭圆G:![]() 的右焦点为F,过F的直线l交椭圆于A、B两点,直线与l不与坐标轴平行,若AB的中点为N,O为坐标原点,直线ON交直线x=3于点M.
的右焦点为F,过F的直线l交椭圆于A、B两点,直线与l不与坐标轴平行,若AB的中点为N,O为坐标原点,直线ON交直线x=3于点M.
(1)求证:MF⊥l;
(2)求![]() 的最大值,
的最大值,
【答案】(1)证明见解析(2)![]()
【解析】
(1)由题意的方程可得右焦点F的坐标,由题意设直线l的方程与椭圆联立可得两根之和,求出AB的中点N的坐标,进而可得直线ON的斜率,求出直线ON的方程,令x=3可得M的纵坐标,即求出M的坐标,求出直线MF的斜率可证得与直线l的斜率互为负倒数,所以可证得MF垂直直线l;
(2)由(1)MF,AB的值,求出两者之比,由均值不等式可得![]() 的最大值.
的最大值.
(1)由椭圆的方程开发右焦点F的坐标(2,0),
有题意设直线AB的方程为x=my+2,设A(x1,y2),B(x2,y2),
![]() 整理可得(3+m2)y2+4my﹣2=0,y1+y2
整理可得(3+m2)y2+4my﹣2=0,y1+y2![]() ,y1y2
,y1y2![]() ,
,
所以AB的中点N的纵坐标yN![]() ,代入直线AB的方程可得N的横坐标xN
,代入直线AB的方程可得N的横坐标xN![]() 2
2![]() ,即N(
,即N(![]() ,
,![]() ),
),
所以kON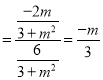 ,
,
所以直线ON的方程为:y![]() x,令x=3,所以y=﹣m,
x,令x=3,所以y=﹣m,
即M(3,﹣m),
所以kMF![]() m,而
m,而![]()
![]() ,所以kMF
,所以kMF![]() =﹣1,
=﹣1,
所以MF⊥l;
(2)由(1)可得|MF|![]() ,
,
|AB|![]() |y1﹣y2|
|y1﹣y2|![]() ,
,
所以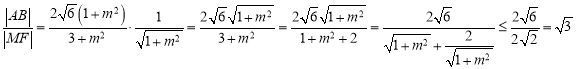 ,当且仅当
,当且仅当![]() ,即m=±1时取等号.
,即m=±1时取等号.
所以![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
