题目内容
1、函数y=xcosx-sinx的导数为（ ）
分析：直接利用积的求导法则进行计算，其中x′=1，sin′x=cosx，cos'x=-sinx
解答：解：y′=（xcosx）′-（sinx）'
=（x）′cosx+x（cosx）′-cosx
=cosx-xsinx-cosx
=-xsinx．
故选B．
=（x）′cosx+x（cosx）′-cosx
=cosx-xsinx-cosx
=-xsinx．
故选B．
点评：计算时对基本函数的求导公式和法则的掌握是做题的关键．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
函数y=-xcosx的部分图象是（ ）
A、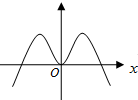 | B、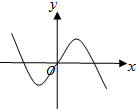 | C、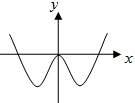 | D、 |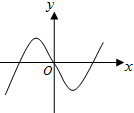
函数y=xcosx-sinx在下面哪个区间内是增函数（ ）
A、（
| ||||
| B、（π，2π） | ||||
C、（
| ||||
| D、（2π，3π） |