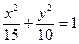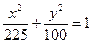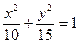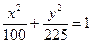题目内容
(本小题满分14分)
设椭圆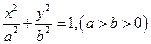 的左右焦点分别为
的左右焦点分别为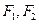 ,离心率
,离心率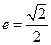 ,点
,点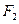 在直线
在直线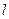 :
: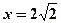 的左侧,且F2到l的距离为
的左侧,且F2到l的距离为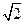 。
。
(1)求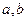 的值;
的值;
(2)设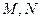 是
是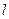 上的两个动点,
上的两个动点,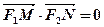 ,证明:当
,证明:当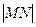 取最小值时,
取最小值时,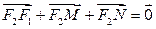
设椭圆
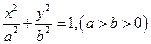 的左右焦点分别为
的左右焦点分别为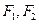 ,离心率
,离心率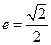 ,点
,点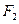 在直线
在直线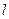 :
: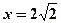 的左侧,且F2到l的距离为
的左侧,且F2到l的距离为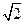 。
。(1)求
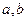 的值;
的值;(2)设
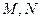 是
是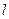 上的两个动点,
上的两个动点,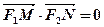 ,证明:当
,证明:当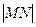 取最小值时,
取最小值时,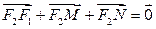
(1)因为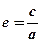 ,
,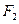 到
到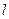 的距离=
的距离=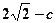 ,所以由题设得
,所以由题设得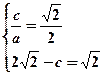
解得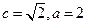 由
由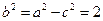 ,得
,得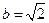 …………5分
…………5分
(2)由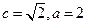 得
得 ,
,
因为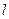 的方程为
的方程为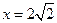 ,故可设
,故可设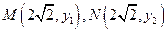 …………7分
…………7分
由知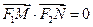 知
知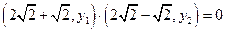
得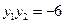 ,所以
,所以 …………9分
…………9分
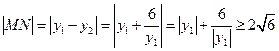
当且仅当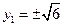 时,上式取等号,此时
时,上式取等号,此时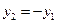 …………12分
…………12分
所以,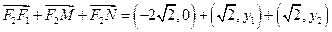
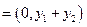
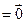
…………14分
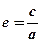 ,
,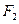 到
到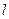 的距离=
的距离=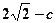 ,所以由题设得
,所以由题设得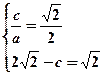
解得
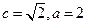 由
由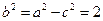 ,得
,得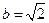 …………5分
…………5分(2)由
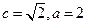 得
得 ,
,因为
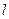 的方程为
的方程为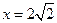 ,故可设
,故可设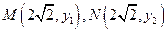 …………7分
…………7分由知
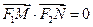 知
知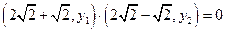
得
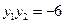 ,所以
,所以 …………9分
…………9分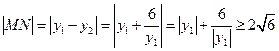
当且仅当
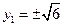 时,上式取等号,此时
时,上式取等号,此时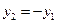 …………12分
…………12分所以,
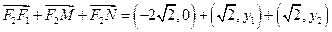
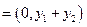
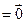
…………14分
略

练习册系列答案
相关题目
 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.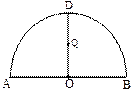
 使
使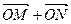 与
与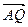 平行,若平行,求出直线
平行,若平行,求出直线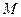 过点
过点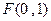 ,且与定圆
,且与定圆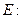
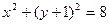 内切,动圆圆心
内切,动圆圆心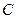 ,点
,点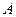 的坐标为
的坐标为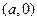 .
.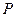 为曲线
为曲线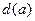 ;
;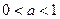 时,在(2)的条件下,设
时,在(2)的条件下,设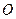 是坐标原点,
是坐标原点,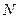 是曲线
是曲线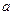 的点,记△
的点,记△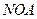 的面积为
的面积为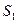 ,以
,以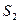 .若正数
.若正数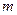 满足
满足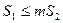 ,问
,问 是椭圆
是椭圆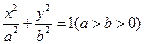 的两个焦点,
的两个焦点, 为坐标原点,点
为坐标原点,点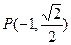 在椭圆上,且
在椭圆上,且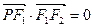 ,⊙
,⊙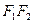 为直径的圆,直线
为直径的圆,直线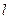 :
: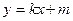 与⊙
与⊙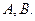
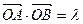 ,且满足
,且满足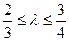 时,求弦长
时,求弦长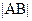 的取值范围.
的取值范围.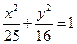 上一点
上一点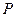 到左准线的距离为10,
到左准线的距离为10,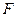 是该椭圆的左焦点,若点
是该椭圆的左焦点,若点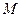 满足
满足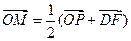 ,则
,则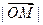 = .
= .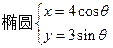 左焦点的坐标是_________________
左焦点的坐标是_________________ 为椭圆
为椭圆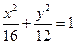 上任一点,当
上任一点,当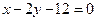 的距离的最小时,点
的距离的最小时,点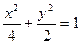 的左、右焦点,l是椭圆的一条准线,点P在l上,则∠EPF的最大值是( )
的左、右焦点,l是椭圆的一条准线,点P在l上,则∠EPF的最大值是( )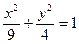 有相同的焦点的椭圆的方程为( )
有相同的焦点的椭圆的方程为( )