Question

18．在四面体ABCD中，已知∠ADB=∠BDC=∠CDA=60°，AD=BD=3，CD=2，则四面体ABCD的外接球的半径为$\sqrt{3}$，内切球的半径为$\frac{126\sqrt{2}-12\sqrt{114}}{71}$．

Answer 1

分析 设四面体ABCD的外接球球心为O，则O在过△ABD的外心N且垂直于平面ABD的垂线上，且点N为△ABD的中心．设P，M分别为AB，CD的中点，则N在DP上，且ON⊥DP，OM⊥CD，从而可求DM，MN，进而可求四面体ABCD的外接圆的直径，即可求得四面体ABCD的外接球的半径；利用等体积，即可求出四面体ABCD的内切球的半径．

解答 解：设四面体ABCD的外接球球心为O，则O在过△ABD的外心N且垂直于平面ABD的垂线上．
由题设知，△ABD是正三角形，则点N为△ABD的中心．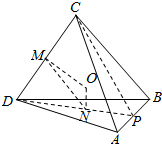
设P，M分别为AB，CD的中点，则N在DP上，且ON⊥DP，OM⊥CD．
因为∠CDA=∠CDB=∠ADB=60°，设CD与平面ABD所成角为θ，
∴cosθ=$\frac{1}{\sqrt{3}}$，sinθ=$\frac{\sqrt{2}}{\sqrt{3}}$．
在△DMN中，DM=$\frac{1}{2}$CD=1，DN=$\frac{2}{3}$•DP=$\sqrt{3}$．
由余弦定理得MN²=1²+（$\sqrt{3}$）²-2•1•$\sqrt{3}$•$\frac{1}{\sqrt{3}}$=2，
故MN=$\sqrt{2}$．
∴四面体ABCD的外接圆的半径OD=$\frac{MN}{sinθ}$=$\sqrt{3}$．
故四面体ABCD的外接球的半径R=$\sqrt{3}$．
AC=BC=$\sqrt{9+4-2×3×2×\frac{1}{2}}$=$\sqrt{7}$，∴CP=$\sqrt{7-\frac{9}{4}}$=$\frac{\sqrt{19}}{2}$，
△CDP中，cos∠CDP=$\frac{\sqrt{3}}{3}$，DP=$\frac{3\sqrt{3}}{2}$，CD=2，∴S_△CDP=$\frac{1}{2}×2×\frac{3\sqrt{3}}{2}×\frac{2\sqrt{2}}{3}$=$\sqrt{6}$，
设内切球的半径为r，则由等体积可得$\frac{1}{3}$×（$\frac{\sqrt{3}}{4}$×9+2×$\frac{1}{2}×2×3×\frac{\sqrt{3}}{2}$+$\frac{1}{2}×3$×$\frac{\sqrt{19}}{2}$）r=$\frac{1}{2}$×$\sqrt{6}$×3，
∴r=$\frac{126\sqrt{2}-12\sqrt{114}}{71}$．
故答案为：$\sqrt{3}$，$\frac{126\sqrt{2}-12\sqrt{114}}{71}$．

点评 本题考查四面体ABCD的外接球、内切球的半径，考查学生的计算能力，确定四面体ABCD的外接球球心位置是关键．