题目内容

若二次函数f（x）=ax2+bx+c的对称轴为x=1，且其图象过点（2，0），则
f(-1)
f(1)
的值是（　　）
分析：先根据已知条件求出a，b，c的值或之间的关系，再代入f（x）=ax2+bx+c对其进行整理；最后代入所求即可得到结论．
解答：解：由条件得：
-
b
2a
=1
f(2)=0
⇒
b=-2a
4a+2b+c=0
⇒
b=-2a
c=0

所以f（x）=ax2-2ax=ax（x-2）．
∴
f(-1)
f(1)
=
a•(-1)•(-1-2)
a•1•(1-2)
=
3a
-a
=-3．
故选：A
点评：本题主要考查二次函数的性质以及函数的值．在解决关于二次函数的题目时，要注意从题中条件中找到对应的结论，比如本题中，由对称轴为x=1得到b=-2a．
练习册系列答案
相关题目
若二次函数f（x）=ax2-4x+c的值域为[0，+∞），则
a
c2+4
+
c
a2+4
的最小值为
 
．
若二次函数f（x）=x2+bx+c满足f（2）=f（-2），且函数的f（x）的一个零点为1．
（Ⅰ） 求函数f（x）的解析式；
（Ⅱ）对任意的x∈[
12
，+∞)，4m2f（x）+f（x-1）≥4-4m2恒成立，求实数m的取值范围．
若二次函数f （x）=ax2+bx+c（a≠0）的部分对应值如下所示：
x -2 1 3
f （x） 0 -6 0
则不等式f （x）＜0的解集为（　　）
若二次函数f（x）=ax2+bx+1（a，b为实数且x∈R）．
（1）若函数f（x）为偶函数，且满足f（x）=2x有两个相等实根，求a，b的值；
（2）若f（-1）=0，且函数f（x）的值域为[0，+∞），求函数f（x）的表达式；
（3）在（2）的条件下，当x∈[-2，2]时，g（x）=f（x）-kx是单调函数，求实数k的取值范围．
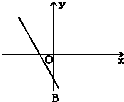精英家教网若二次函数f（x）=ax2+bx的导函数f′（x）的图象如图所示，则二次函数f（x）的顶点在（　　）
A、第四象限B、第三象限C、第二象限D、第一象限

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网