题目内容
若二次函数f (x)=ax2+bx+c(a≠0)的部分对应值如下所示:
|
分析:题目给出了二次函数模型,可以对照给出的对应值表取几组值代入函数模型,求解出a、b、c的值,代入后不等式ax2+bx+c<0的解集可求;
解答:解:由于函数过点(-2,0),(3,0)
则y=ax2+bx+c=a(x+2)(x-3),
又由函数f (x)过点(1,-6)
则a(1+2)(1-3)=-6,解得a=1
故y=(x+2)(x-3)
则f(x)<0的解集是:(-2,3).
故答案为 A
则y=ax2+bx+c=a(x+2)(x-3),
又由函数f (x)过点(1,-6)
则a(1+2)(1-3)=-6,解得a=1
故y=(x+2)(x-3)
则f(x)<0的解集是:(-2,3).
故答案为 A
点评:本题考查了一元二次不等式的解法,考查了数学模型法,解答此题的关键是现根据给出的对应值表求出三个系数,属基础题.

练习册系列答案
相关题目
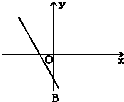 若二次函数f(x)=ax2+bx的导函数f′(x)的图象如图所示,则二次函数f(x)的顶点在( )
若二次函数f(x)=ax2+bx的导函数f′(x)的图象如图所示,则二次函数f(x)的顶点在( )| A、第四象限 | B、第三象限 | C、第二象限 | D、第一象限 |