题目内容
若二次函数f(x)=ax2-4x+c的值域为[0,+∞),则| a |
| c2+4 |
| c |
| a2+4 |
分析:由题意可知,a>0,△=0,从而求出ac=4,将所求式子中的4代换成ac,利用裂项法进行整理,进而利用均值不等式求出最小值.
解答:解:∵二次函数f(x)=ax2-4x+c(x∈R)的值域为[0,+∞),
∴a>0,△=16-4ac=0,
∴a>0,c>0,ac=4,
∴
+
=
+
=
+
=
-
+
-
=
+
-
≥2
-
=
,
当且仅当a=c=2时取等号.
故答案为
.
∴a>0,△=16-4ac=0,
∴a>0,c>0,ac=4,
∴
| a |
| c2+4 |
| c |
| a2+4 |
=
| a |
| c2+ac |
| c |
| a2+ac |
=
| a |
| c(a+c) |
| c |
| a(a+c) |
=
| 1 |
| c |
| 1 |
| a+c |
| 1 |
| a |
| 1 |
| a+c |
=
| 1 |
| a |
| 1 |
| c |
| 2 |
| a+c |
≥2
|
| 2 | ||
2
|
| 1 |
| 2 |
当且仅当a=c=2时取等号.
故答案为
| 1 |
| 2 |
点评:利用基本不等式求函数最值是高考考查的重点内容,对不符合基本不等式形式的应首先变形,然后必须满足三个条件:一正、二定、三相等.同时注意裂项法的运用.

练习册系列答案
相关题目
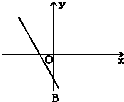 若二次函数f(x)=ax2+bx的导函数f′(x)的图象如图所示,则二次函数f(x)的顶点在( )
若二次函数f(x)=ax2+bx的导函数f′(x)的图象如图所示,则二次函数f(x)的顶点在( )| A、第四象限 | B、第三象限 | C、第二象限 | D、第一象限 |