题目内容
若二次函数f(x)=ax2+bx+1(a,b为实数且x∈R).
(1)若函数f(x)为偶函数,且满足f(x)=2x有两个相等实根,求a,b的值;
(2)若f(-1)=0,且函数f(x)的值域为[0,+∞),求函数f(x)的表达式;
(3)在(2)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
(1)若函数f(x)为偶函数,且满足f(x)=2x有两个相等实根,求a,b的值;
(2)若f(-1)=0,且函数f(x)的值域为[0,+∞),求函数f(x)的表达式;
(3)在(2)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
分析:(1)利用函数f(x)为偶函数,求出b,利用f(x)=2x有两个相等实根,△=0,求出a,即可得到a,b的值;
(2)若f(-1)=0,推出a,b的一个关系式,利用函数f(x)的值域为[0,+∞),得到a,b,的关系式,然后求a,b,得到函数f(x)的表达式;
(3)通过(2)的条件,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,利用二次函数的对称轴,求实数k的取值范围.
(2)若f(-1)=0,推出a,b的一个关系式,利用函数f(x)的值域为[0,+∞),得到a,b,的关系式,然后求a,b,得到函数f(x)的表达式;
(3)通过(2)的条件,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,利用二次函数的对称轴,求实数k的取值范围.
解答:解:(1)因为函数是偶函数,所以b=0,
因为f(x)=2x有两个相等实根,
即ax2+1=2x.有△=0,
所以a=1.
(2)∵f(-1)=0,∴a-b+1=0,
又x∈R,f(x)≥0恒成立.
∴
,
∴b2-4(b-1)≤0,
∴b=2,a=1,
∴f(x)=x2+2x+1.
(3)g(x)=f(x)-kx
=x2+2x+1-kx=x2+(2-k)x+1
=(x+
)2+1-
,
当
≥2或
≤-2时,
即k≥6或k≤-2时,g(x)是单调函数.
因为f(x)=2x有两个相等实根,
即ax2+1=2x.有△=0,
所以a=1.
(2)∵f(-1)=0,∴a-b+1=0,
又x∈R,f(x)≥0恒成立.
∴
|
∴b2-4(b-1)≤0,
∴b=2,a=1,
∴f(x)=x2+2x+1.
(3)g(x)=f(x)-kx
=x2+2x+1-kx=x2+(2-k)x+1
=(x+
| 2-k |
| 2 |
| (2-x)2 |
| 4 |
当
| 2-k |
| 2 |
| 2-k |
| 2 |
即k≥6或k≤-2时,g(x)是单调函数.
点评:本题考查一元二次方程的根的分布与系数的关系,函数奇偶性的性质,二次函数的性质的应用,考查计算能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
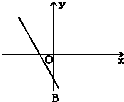 若二次函数f(x)=ax2+bx的导函数f′(x)的图象如图所示,则二次函数f(x)的顶点在( )
若二次函数f(x)=ax2+bx的导函数f′(x)的图象如图所示,则二次函数f(x)的顶点在( )| A、第四象限 | B、第三象限 | C、第二象限 | D、第一象限 |