题目内容
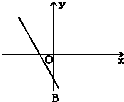若二次函数f（x）=ax2+bx的导函数f′（x）的图象如图所示，则二次函数f（x）的顶点在（ ）| A、第四象限 | B、第三象限 | C、第二象限 | D、第一象限 |
分析：根据一次函数图象确定出a＜0，b＜0，则二次函数图象的开口方向向下，对称轴为直线x=-
＜0，再根据函数过原点，即可确定出顶点在第二象限．
| a |
| 2b |
解答：解：∵二次函数f（x）=ax2+bx的导函数f′（x）=2ax+b，
∴a＜0，b＜0，
∴二次函数图象的开口方向向下，对称轴为直线x=-
＜0，
又∵二次函数f（x）=ax2+bx过点（0，0），
∴二次函数f（x）的顶点的纵坐标大于0，
故二次函数f（x）的顶点在第二象限．
故选：C．
∴a＜0，b＜0，
∴二次函数图象的开口方向向下，对称轴为直线x=-
| a |
| 2b |
又∵二次函数f（x）=ax2+bx过点（0，0），
∴二次函数f（x）的顶点的纵坐标大于0，
故二次函数f（x）的顶点在第二象限．
故选：C．
点评：本题考查了二次函数的图象，一次函数的图象，根据图形确定出a、b的正负情况是解题的关键．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目