题目内容
【题目】某市电视台为了提高收视率而举办有奖问答活动,随机对该市15~65岁的人群抽样了 ![]() 人,回答问题统计结果及频率分布直方图如图表所示.
人,回答问题统计结果及频率分布直方图如图表所示.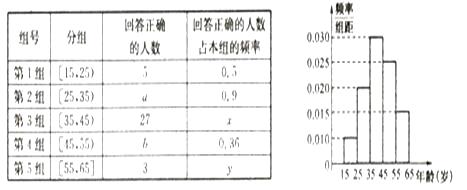
(1)分别求出 ![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
【答案】
(1)解:由频率表中第一组数据可知,第一组总人数为 ![]() ,
,
再结合频率分布直方图可知 ![]() ,
,![]() ,
,![]() ,
,
x=![]()
y=![]()
![]()
a=18;b=9;x=0.9;y=0.2
(2)解:第二,三,四组中回答正确的共有 ![]() 人,所以利用分层抽样在
人,所以利用分层抽样在 ![]() 人中抽取
人中抽取 ![]() 人,每组分别抽取的人数为:
人,每组分别抽取的人数为:
第二组: ![]() 人,
人,
第三组: ![]() 人,
人,
第四组: ![]() 人
人
第2,3,4组每组应各抽取2,3,1人.
(3)解:设第二组的 ![]() 人为
人为 ![]() ,第三组的
,第三组的 ![]() 人为
人为 ![]() ,第四组的
,第四组的 ![]() 人为
人为 ![]() ,则从
,则从 ![]() 人中抽
人中抽 ![]() 人所有可能的结果有:
人所有可能的结果有:![]()
![]() 共
共 ![]() 个基本
个基本
事件,其中第二组至少有一人被抽中的有![]() 这
这 ![]() 个基本事件.所以第二组至少有一人获得幸运奖的概率为
个基本事件.所以第二组至少有一人获得幸运奖的概率为 ![]() .
.
【解析】(1)结合频率分布表和直方图的性质求a,b,x,y的值;
(2)利用分层抽样的特点求各级组应抽取的人数;
(3)古典概型,先列出所有基本事件,找出合符条件的基本事件的总数,进而求概率.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案【题目】某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表.
组号 | 分组 | 频率 |
第1组 | [160,165) | 0.05 |
第2组 |
| 0.35 |
第3组 |
| 0.3 |
第4组 |
| 0.2 |
第5组 |
| 0.1 |
合计 | 1.00 | |
(Ⅰ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样的方法抽取6名学生进行体能测试,问第3,4,5组每组各应抽取多少名学生进行测试;
(Ⅱ)在(Ⅰ)的前提下,学校决定在6名学生中随机抽取2名学生进行引体向上测试,求第3组中至少有一名学生被抽中的概率;
(Ⅲ)试估计该中学高三年级男生身高的中位数位于第几组中,并说明理由.