Question

（本小题满分14分）

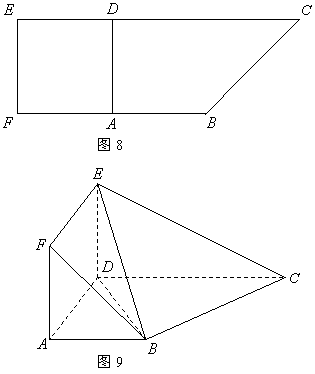
如图8，在直角梯形中，，，且．

现以为一边向形外作正方形，然后沿边将正方形翻折，使平面

与平面互相垂直，如图9．

（1）求证：平面平面；

（2）求平面与平面所成锐二面角的大小．

 

Answer 1

（本小题满分14分）

证明（1）（法一）因为平面平面，

且平面平面，

又在正方形中，，

所以，平面．  ………………2分

而平面，

所以，．         ………………3分

在直角梯形中，,，

，

所以，，

所以，．          ………………4分

又，平面，，

所以，平面．     ………………6分

而平面，

所以，平面平面． ……………7分

（法二）同法一，得平面．               …………………………2分

以为原点，，，分别为，轴，建立空间直角坐标系．

则，，，．      …………………………3分

所以，， ，,

，，

所以，，．                      …………………………………5分

又，不共线，，平面，

所以，平面．                            …………………………6分

而平面，

所以，平面平面．                      …………………………7分

解 （2）（法一）因为，平面，平面，

所以，平面．                          …………………………9分

因为平面与平面有公共点，

所以可设平面平面，．

因为平面，平面，平面平面，

所以．                                     ………………………10分

从而，，

又，且，，所以为中点，也为正方形．  12分

易知平面，所以，．

所以，是平面与平面所成锐二面角的平面角，

而，

所以平面与平面所成锐二面角为．      …………………………14分

（法二）由（1）知，平面的一个法向量是．  ………………9分

设平面的一个法向量为，

因为，

所以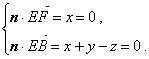， 取，得，所以．………………11分

设平面与平面所成锐二面角为，

则．                 ………………………………13分

所以平面与平面所成锐二面角为．     …………………………14分