题目内容
【题目】在等比数列{an}中，a1=1，且a2是a1与a3﹣1的等差中项．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足 
．求数列{bn}的前n项和 
．
【答案】
（1）解：设等比数列{an}的公比为q，
a2是a1与a3﹣1的等差中项，即有a1+a3﹣1=2a2，
即为1+q2﹣1=2q，解得q=2，
即有an=a1qn﹣1=2n﹣1
（2）解： 
=an+ 
=2n﹣1+（ 
﹣ 
），
数列{bn}的前n项和 
=（1+2+22+…+2n﹣1）+（1﹣ 
+ ﹣ 
+ ﹣ 
+…+ ﹣ ）
= 
+1﹣ =2n﹣
【解析】（1）设等比数列{an}的公比为q，运用等差数列的性质和等比数列的通项公式，解方程可得公比q，即可得到所求通项公式；（2）化简bn=2n﹣1+（ ﹣ ），运用分组求和和裂项相消求和，化简即可得到所求和．
【考点精析】利用等比数列的通项公式（及其变式）和数列的前n项和对题目进行判断即可得到答案，需要熟知通项公式：
；数列{an}的前n项和sn与通项an的关系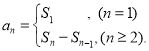
．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
