Question

【题目】已知椭圆E的中心在坐标原点，焦点在x轴上，离心率为 ，且椭圆E上一点到两个焦点距离之和为4；l1 ， l2是过点P（0，2）且互相垂直的两条直线，l1交E于A，B两点，l2交E交C，D两点，AB，CD的中点分别为M，N．
（1）求椭圆E的方程；
（2）求l1的斜率k的取值范围；
（3）求 的取值范围．

Answer 1

【答案】
（1）解：设椭圆方程为 ，

由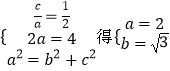

∴椭圆方程为 ；

（2）解：由题意知，直线l1的斜率存在且不为零

∵ ，∴ ．

由 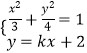消去y并化简整理，

得（3+4k2）x2+16kx+4=0

根据题意，△=（16k）2﹣16（3+4k2）＞0，解得 ．

同理得 ，

∴ ；

（3）解：设A（x1，y1），B（x2，y2），M（x0，y0）

那么 ，∴ ，∴

同理得 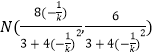，即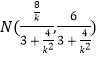

∴

∵ ，∴

∴

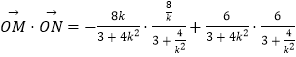
即 的取值范围是

【解析】（1）设椭圆的标准方程，根据离心率求得a和c关系，进而根据a求得b，则椭圆的方程可得．（2）由题意知，直线l1的斜率存在且不为零设直线l1和l2的方程，分别于椭圆方程联立消去y，根据判别式求得k的范围，最后综合可得答案．（3）设A（x1 ， y1），B（x2 ， y2），M（x0 ， y0），根据韦达定理求得x0和y0的表达式，进而表示M和N的坐标，最后表示出 根据k的范围确定答案．