题目内容
7.已知函数y=x2-2011x+2012与x轴的交点坐标是(m,0)、(n,0),则(m2-2012m+2012)(n2-2012n+2012)的值为( )| A. | 2011 | B. | 20122 | C. | 2011×2012 | D. | 2012 |
分析 将x=m,n代入函数的表达式,求出m2-2011m+2012=0,n2-2011n+2012=0,再代入求出积即可.
解答 解:∵函数y=x2-2011x+2012与x轴交点是(m,0),(n,0),
∴m,n是方程x2-2011x+2012=0的两个根,
即m2-2011m+2012=0,n2-2011n+2012=0,
∴mn=2012,
(m2-2012m+2012)(n2-2012n+2012)
=(m2-2011m+2012-m)(n2-2011n+2012-n)
=mn
=2012.
故选:D.
点评 本题考查了二次函数的性质,考查韦达定理,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.函数f(x)=ax(a>0,且a≠1),若f(3a)>$\sqrt{a}$,则实数a的取值范围为( )
| A. | (0,$\frac{1}{2}$)∪(1,+∞) | B. | (0,$\frac{1}{2}$)∪(1,2) | C. | (0,$\frac{1}{6}$)∪(1,+∞) | D. | (0,$\frac{1}{6}$)∪(1,6) |
19.某运动员每次投篮的命中率为60%,现采用随机模拟的方法估计该运动员3次投篮恰好命中2次的概率,先由计算器产生0到9之间取整数值的随机表,指定1,2,3,4表示命不中,5,6,7,8,9,0表示命中,再以每3个随机数为一组,代表3次投篮的结果,经随机模拟产生了如下10组随机数:
907 966 191 925 271 932 812 458 569 683
据此估计,该运动员3次投篮恰好命中2次的概率为( )
907 966 191 925 271 932 812 458 569 683
据此估计,该运动员3次投篮恰好命中2次的概率为( )
| A. | 0.35 | B. | 0.30 | C. | 0.6 | D. | 0.70 |
16.为了了解泉州市新装修房屋室内甲醛含量是否合格,某检测单位随机抽取了20户新装修的房屋进行检测,得到如下结果:(单位:mg/m3)
A0.02 0.03 0.03 0.04 0.05 0.05 0.05 0.06 0.06 0.06
A0.06 0.07 0.07 0.08 0.09 0.10 0.10 0.11 0.13 0.14
(Ⅰ)完成下列表格
(Ⅱ)参照测量条件与国家相关标准,空气中甲醛含量不超过0.08mg/m3的房屋可认定为“空气质量合格”,否则为“空气质量不合格”.若检测单位从“空气质量不合格”的房屋户主中随机抽取2名进行访谈,求所选中的两户房屋空气中,甲醛含量均在(0.08,0.12]的概率.
A0.02 0.03 0.03 0.04 0.05 0.05 0.05 0.06 0.06 0.06
A0.06 0.07 0.07 0.08 0.09 0.10 0.10 0.11 0.13 0.14
(Ⅰ)完成下列表格
| 分组 | 频数 | 频率 |
| [0.00,0.04] | 4 | 0.2 |
| (0.04,0.08] | 10 | 0.5 |
| (0.08,0.12] | 4 | 0.2 |
| (0.12,0.16] | 2 | 0.1 |
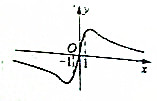 若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的取值范围是(1,2).
若函数f(x)=$\frac{(2-m)x}{{x}^{2}+m}$的图象如图所示,则m的取值范围是(1,2).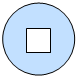 欧阳修《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.可见“行行出状元”,卖油翁的技艺让人叹为观止,如右图铜钱是直径为4cm的圆形,正中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴是直径为0.2cm的球),记“油滴不出边界”为事件A,“油滴整体正好落入孔中”为事件B.则P(B|A)=$\frac{64}{361π}$(不作近似值计算).
欧阳修《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.可见“行行出状元”,卖油翁的技艺让人叹为观止,如右图铜钱是直径为4cm的圆形,正中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴是直径为0.2cm的球),记“油滴不出边界”为事件A,“油滴整体正好落入孔中”为事件B.则P(B|A)=$\frac{64}{361π}$(不作近似值计算).