题目内容
10．在抽查某产品尺寸的过程中，将其尺寸分成若干组，[12.025，12.045]是其中一组，抽查出的个数在该组上的频率为m，则该组上的直方图的高h为（ ）| A． | 0.02m | B． | m | C． | 50m | D． | 12.035m |
分析 频率分布直方图中，频率=组距×对应直方图的高，由此列出等式，求出h的值．
解答 解：在频率分布直方图中，频率=组距×对应直方图的高，
∴m=（12.045-12.025）h，
∴h=$\frac{m}{12.045-12.025}$=50m．
故选：C．
点评 本题考查了在频率分布直方图中求频率的应用问题，是基础题目．
练习册系列答案
相关题目
20．已知i为虚数单位，（2+i）z=1+2i，则z的共轭复数$\overline{z}$=（ ）
| A． | $\frac{4}{5}$+$\frac{3}{5}$i | B． | $\frac{4}{5}$-$\frac{3}{5}$i | C． | $\frac{4}{3}$+i | D． | $\frac{4}{3}$-i |
1．在△ABC中，已知a2-b2-c2=$\sqrt{2}$bc，则角B+C等于（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{3π}{4}$ | C． | $\frac{5π}{4}$ | D． | $\frac{π}{4}$或$\frac{3π}{4}$ |
18．据气象预报，某地区下月有小洪水的概率为0.2，有大洪水的概率为0.05．该地区某工地上有一台大型设备，两名技术人员就保护设备提出了以下两种方案．
方案一：建一保护围墙，需花费4000元，但围墙无法防止大洪水，当大洪水来临时，设备会受损，损失费为30000元．
方案二：不采取措施，希望不发生洪水，此时小洪水来临将损失15000元，大洪水来临将损失30000元．
以下说法正确的是（ ）
方案一：建一保护围墙，需花费4000元，但围墙无法防止大洪水，当大洪水来临时，设备会受损，损失费为30000元．
方案二：不采取措施，希望不发生洪水，此时小洪水来临将损失15000元，大洪水来临将损失30000元．
以下说法正确的是（ ）
| A． | 方案一的平均损失比方案二的平均损失大 | |
| B． | 方案二的平均损失比方案一的平均损失大 | |
| C． | 方案一的平均损失与方案二的平均损失一样大 | |
| D． | 方案一的平均损失与方案二的平均损失无法计算 |
5．
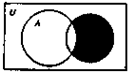已知集合A={x∈Z||x|≤1}，B={x|x2-2x=0}，若全集U=R，则图中的阴影部分表示的集合为（ ）
已知集合A={x∈Z||x|≤1}，B={x|x2-2x=0}，若全集U=R，则图中的阴影部分表示的集合为（ ）| A． | {-1} | B． | {2} | C． | {1，2} | D． | {0，2} |
15．已知1，2，3，4，x1，x2，x3的平均数是8，那么x1+x2+x3的值是（ ）
| A． | 14 | B． | 22 | C． | 32 | D． | 46 |
19．计算sin（-240°）的值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $-\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $-\frac{{\sqrt{3}}}{2}$ |
20．采用系统抽样的方法从2005个个体中抽取一个容量为50的样本，则抽样间隔和随机剔除的个体数分别为
（ ）
（ ）
| A． | 40，5 | B． | 50，5 | C． | 5，40 | D． | 5，50 |