题目内容
【题目】
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
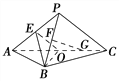
(Ⅰ)设G是OC的中点,证明:FG∥平面BOE;
(Ⅱ)证明:在△ABO内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离.
【答案】(Ⅰ)见解析;(Ⅱ) ![]()
【解析】试题分析:
(1)建立空间直角坐标系,利用题意结合平面的法向量和直线的方向向量可得FG∥平面BOE;
(2)设出点的坐标,利用空间直角坐标系可得点M到OA,OB的距离为![]() .
.
试题解析:
(Ⅰ)如图,连接OP,易知OB,OC,OP两两垂直,以点O为坐标原点,分别以OB,OC,OP所在直线为x轴,y轴,x轴,建立空间直角坐标系O-xyz,
则O(0,0,0),A(0,-8,0),B(8,0,0),C(0,8,0),P(0,0,6),E(0,-4,3),F(4,0,3).

由题意,得G(0,4,0)
因为![]() =(8,0,0),
=(8,0,0),![]() =(0,-4,3),
=(0,-4,3),
所以平面BOE的一个法向量为n=(0,3,4).
由![]() =(-4,4,-3),得n·
=(-4,4,-3),得n·![]() =0,即n⊥
=0,即n⊥![]() .
.
又直线FG不在平面BOE内,所以FG∥平面BOE.
(Ⅱ)设点M的坐标为(x0,y0,0),
则![]() =(x0-4,y0,-3).
=(x0-4,y0,-3).
所FM⊥平面BOE,所以![]() ∥n.
∥n.
因此x0=4,y0=-![]() ,即点M的坐标是(4,-
,即点M的坐标是(4,-![]() ,0).
,0).
在平面直角坐标系xOy中,△AOB的内部区域可表示为不等式组 
经检验,点M的坐标满足上述不等式组,所以在△AOB内存在一点M, 使FM⊥平面BOE.由点M的坐标得点M到OA,OB的距离分别为4,![]() .
.

练习册系列答案
相关题目