题目内容
【题目】如图,在△ABC中,AB=2,cosB= ![]() ,点D在线段BC上.
,点D在线段BC上. 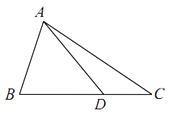
(1)若∠ADC= ![]() π,求AD的长;
π,求AD的长;
(2)若BD=2DC,△ABC的面积为 ![]()
![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)在三角形中,∵cosB= ![]() ,∴sinB=
,∴sinB= ![]() .
.
在△ABD中,由正弦定理得 ![]() ,
,
又AB=2, ![]() ,sinB=
,sinB= ![]() .
.
∴AD= ![]()
(2)∵BD=2DC,∴S△ABD=2S△ADC,S△ABC=3S△ADC,
又 ![]() ,∴
,∴ ![]() ,
,
∵S△ABC= ![]() ,∴BC=6,
,∴BC=6,
∵ ![]() ,
, ![]() ,
,
S△ABD=2S△ADC,∴ ![]() ,
,
在△ABC中,由余弦定理得:
AC2=AB2+BC2﹣2ABBCcos∠ABC,∴AC=4 ![]() ,
,
∴ ![]() =2
=2 ![]() =4
=4 ![]()
【解析】(1)求出sinB= ![]() ,由正弦定理得
,由正弦定理得 ![]() ,由此能求出AD.(2)推导出S△ABD=2S△ADC , S△ABC=3S△ADC ,
,由此能求出AD.(2)推导出S△ABD=2S△ADC , S△ABC=3S△ADC , ![]() ,BC=6,从而得到
,BC=6,从而得到 ![]() ,由此利用余弦定理能求出
,由此利用余弦定理能求出 ![]() 的值.
的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目