题目内容
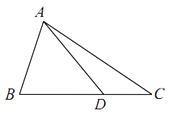
【题目】如图甲所示，BO是梯形ABCD的高，∠BAD=45°，OB=BC=1，OD=3OA，现将梯形ABCD沿OB折起如图乙所示的四棱锥P﹣OBCD，使得PC= 
，点E是线段PB上一动点． 
（1）证明：DE和PC不可能垂直；
（2）当PE=2BE时，求PD与平面CDE所成角的正弦值．
【答案】
（1）证明：如图甲所示，因为BO是梯形ABCD的高，∠BAD=45°，
所以AO=OB
因为BC=1，OD=3OA，可得OD=3，OC= 
如图乙所示，OP=OA=1，OC= ，PC= 
，
所以有OP2+OC2=PC2，所以OP⊥OC
而OB⊥OP，OB∩OC=O，所以OP⊥平面OPD
又OB⊥OD，所以OB、OD、OP两两垂直．故以O为原点，建立空间直角坐标系（如图），则P（0，0，1），C（1，1，0），D（0，3，0）
设E（x，0，1﹣x），其中0≤x≤1，所以 
=（x，﹣3，1﹣x）， 
=（1，1，﹣1），
假设DE和SC垂直，则 
=0，有x﹣3+（1﹣x）（﹣1）=0，解得x=2，
这与0≤x≤1矛盾，假设不成立，所以DE和SC不可能垂直
（2）解：因为PE=2BE，所以 E（ 
，0， 
）
设平面CDE的一个法向量是 
=（x，y，z），
因为 
=（﹣1，2，0）， =（ ，﹣3， ），所以 
取 =（2，1，5）
而 
=（0，3，﹣1），所以|cos＜ ， ＞= 
，
所以PD与平面CDE所成角的正弦值为 ．
【解析】由题可知，可以直接建立空间直角坐标线证明位置关系和计算角．（1）只要证明 =0不成立即可．（2）求出平面CDE的法向量，用向量角的余弦值来求PD与平面CDE所成角的正弦值．
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识，掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点，以及对空间角的异面直线所成的角的理解，了解已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则
．
