题目内容
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,证明
时,证明![]() .
.
【答案】(Ⅰ)详见解析;(Ⅱ)详见解析.
【解析】试题分析:(Ⅰ)易求得函数![]() 的定义域为
的定义域为![]() ,由函数
,由函数![]() ,则
,则![]() ,令
,令![]() 或
或![]() ,即可求得函数
,即可求得函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,
时, ![]() ,要证
,要证![]() ,只需证
,只需证![]() ,所以此问就是求函数
,所以此问就是求函数![]() 在定义域区间的最小值.
在定义域区间的最小值.
试题解析: (Ⅰ)易求得函数![]() 的定义域为
的定义域为![]() ,
,
已知函数![]() ,
,
所以![]() ,
,
令![]() ,即
,即![]()
当![]() 时,
时, ![]() 恒成立,所以函数
恒成立,所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,无单调递减区间。
,无单调递减区间。
当![]() 时,不等式
时,不等式![]() 的解为
的解为![]() 或
或![]()
又因为![]() ,
,
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间为
,单调递减区间为![]()
当![]() 时,不等式
时,不等式![]() 的解为
的解为![]() 或
或![]()
又因为![]() ,
, ![]()
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间为
,单调递减区间为![]()
综上所述,当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,无单调递减区间。
,无单调递减区间。
当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间为
,单调递减区间为![]()
当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间为
,单调递减区间为![]()
(Ⅱ)当![]() 时,
时, ![]()
所以![]()
已知![]()
令![]() ,得
,得![]()
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间为
,单调递减区间为![]()
所以![]()
所以![]()

【题目】根据教育部最新消息,2020年高考数学将是最后一年实行文理分科,由于课程大纲与命题方向出现了变动,试题难度也可能会做出相应调整.为了评估学生在2020年高考复习情况,某中学组织本校540名考生参加市模拟考试,现采用分层抽样的方法从文、理科考生中分别抽取60和30份数学试卷进行成绩分析,得到下面的成绩频数分布表:
分数分组 |
|
|
|
|
|
文科频数 | 12 | 4 | 10 | 11 | 23 |
理科频数 | 3 | 7 | 2 | 10 | 8 |
由此可估计文科考生的不及格人数(90分为及格分数线)大约为( )
A.128B.156C.204D.132
【题目】某银行对某市最近5年住房贷款发放情况(按每年6月份与前一年6月份为1年统计)作了统计调查,得到如下数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
贷款 | 50 | 60 | 70 | 80 | 100 |
(1)将上表进行如下处理:![]() ,
,
得到数据:
| 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
试求![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,再写出
,再写出![]() 与
与![]() 的线性回归方程
的线性回归方程![]() .
.
(2)利用(1)中所求的线性回归方程估算2019年房贷发放数额.
参考公式: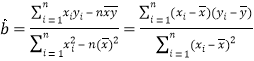 ,
, ![]()