题目内容
8.已知数列{an}的首项a1=1,a2=3,前n项和为Sn,且Sn+1,Sn,Sn-1(n>1)分布是直线l上的点A,B,C的横坐标,$\overrightarrow{AB}=\frac{{2{a_n}+1}}{a_n}\overrightarrow{BC}$,设b1=1,bn+1=log2(an+1)+bn.(1)判断数列{an+1}是否为等比数列,并证明你的结论;
(2)设${C_n}=\frac{{{4^{\frac{{{b_{n+1}}-1}}{n+1}}}}}{{{a_n}{a_{n+1}}}}$,证明:C1+C2+C3+…+Cn<1.
分析 (1)运用向量共线的坐标表示和构造等比数列的思想,由等比数列的通项公式,即可得到;
(2)求出bn的通项,以及cn,并拆成差的形式,再由裂项相消求和,结合不等式的性质,即可得证.
解答 证明:(1)由题意得A,B,C三点共线,
则$\frac{{{S_{n+1}}-{S_n}}}{{{S_n}-{S_{n-1}}}}=\frac{{2{a_n}+1}}{a_n}$,故an+1=2an+1,
所以an+1+1=2(an+1)(n≥2),
所以数列{an+1}是以2为首项,2为公比的等比数列.
则${a_n}+1={2^n}$,所以${a_n}={2^n}-1({n∈{N^*}})$;
(2)证明:由${a_n}={2^n}-1$及bn+1=log2(an+1)+bn,
知bn+1=bn+n,∴${b_n}=1+\frac{{n({n-1})}}{2}$,
则${C_n}=\frac{{{4^{\frac{{{b_{n+1}}-1}}{n+1}}}}}{{{a_n}{a_{n+1}}}}=\frac{2^n}{{({{2^n}-1})({{2^{n+1}}-1})}}=\frac{1}{{{2^n}-1}}-\frac{1}{{{2^{n+1}}-1}}$,
所以$\sum_{i=1}^n{{C_i}=({\frac{1}{2-1}-\frac{2}{{{2^2}-1}}})+({\frac{1}{{{2^2}-1}}-\frac{1}{{{2^3}-1}}})+…+({\frac{1}{{{2^n}-1}}-\frac{1}{{{2^{n+1}}-1}}})}$
=$1-\frac{1}{{{2^{n+1}}-1}}<1$.
点评 本题考查向量共线的坐标表示,以及等比数列的定义和通项公式的运用,考查数列的裂项相消求和以及不等式的性质,属于中档题.

 阅读快车系列答案
阅读快车系列答案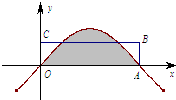 点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示),若图中阴影部分的面积等于矩形OABC的面积,那么边AB的长等于( )
点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示),若图中阴影部分的面积等于矩形OABC的面积,那么边AB的长等于( )| A. | $\frac{1}{π}$ | B. | $\frac{2}{π}$ | C. | $\frac{3}{π}$ | D. | $\frac{4}{π}$ |
| A. | 1.5 | B. | 3 | C. | 0.5 | D. | 3.5 |
| A. | 96 | B. | 108 | C. | 145 | D. | 160 |
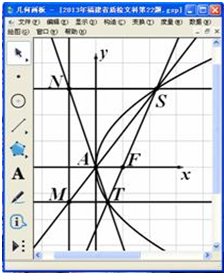 某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.
某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.