题目内容
已知数列(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)证明:对任意的![]() ,
,![]() ,
,![]() ;
;
(Ⅲ)证明:![]() .
.
解法一:(Ⅰ)![]() ,
,![]() ,
,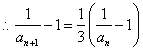 ,
,
又![]() ,
,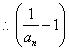 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
![]()
![]() ,
,![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,
,
![]()
![]()

![]()

![]() ,
,![]() 原不等式成立.
原不等式成立.
(Ⅲ)由(Ⅱ)知,对任意的![]() ,有
,有
![]()
![]()
![]() .
.
![]() 取
取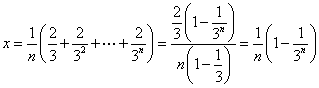 ,
,
则 .
.
![]() 原不等式成立.
原不等式成立.
解法二:(Ⅰ)同解法一.
(Ⅱ)设![]() ,
,
则
![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 当
当![]() 时,
时,![]() 取得最大值
取得最大值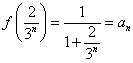 .
.
![]() 原不等式成立.
原不等式成立.
(Ⅲ)同解法一.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知数列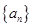 的首项
的首项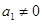 ,其前
,其前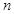 项的和为
项的和为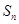 ,且
,且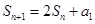 ,则
,则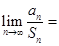
| A.0 | B.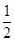 | C.1 | D.2 |
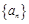 的首项为
的首项为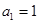 ,且
,且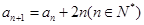 ,则这个数列的通项公式为___________
,则这个数列的通项公式为___________