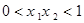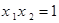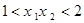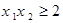题目内容
(本小题满分13分)
(1)证明:函数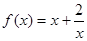 在
在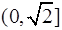 上是减函数,在[
上是减函数,在[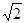 ,+∞)上是增函数;
,+∞)上是增函数;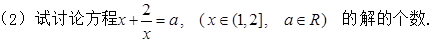
(1)证明:函数
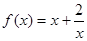 在
在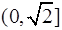 上是减函数,在[
上是减函数,在[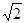 ,+∞)上是增函数;
,+∞)上是增函数;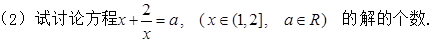
解: (1)证明:见解析;
(2)当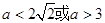 时,方程无解;当
时,方程无解;当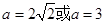 方程有一个解;当
方程有一个解;当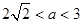 时,方程有两个解.
时,方程有两个解.
(2)当
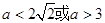 时,方程无解;当
时,方程无解;当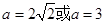 方程有一个解;当
方程有一个解;当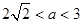 时,方程有两个解.
时,方程有两个解. 本试题主要是考查了二次函数的单调性以及函数与方程的综合运用。
(1)根据但单调性的定义法,设变量,作差,变形定号,下结论。
(2)在第一问的基础上,结合单调性,得到函数的最值,然后分析得到参数的范围。
解: (1)证明:设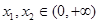 ,且
,且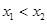
则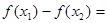
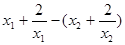 =
=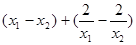 =
=
=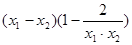 =
=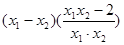 .………4分
.………4分
(ⅰ)若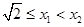 ,
,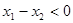 且
且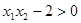 ,
,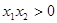 ,所以
,所以 ,
,
即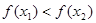 .所以函数
.所以函数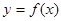 在区间[
在区间[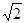 ,+∞)上单调递增.………6分
,+∞)上单调递增.………6分
(ⅱ)若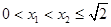 ,则
,则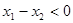 且
且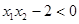 ,
,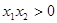 ,
,
所以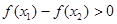 ,即
,即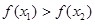 .所以函数
.所以函数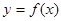 在区间[
在区间[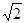 ,+∞)上单调递减.………………………………8分
,+∞)上单调递减.………………………………8分
(2)由(1)知函数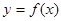 在区间(1,
在区间(1,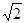 )上单调递减,在区间[
)上单调递减,在区间[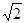 ,2]上单调递增
,2]上单调递增
所以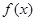 的最小值=
的最小值= ,
,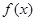 的最大值=
的最大值=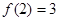 ……………………10分
……………………10分
故当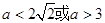 时,方程无解;当
时,方程无解;当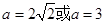 方程有一个解;当
方程有一个解;当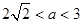 时,方程有两个解.………………………………………13分
时,方程有两个解.………………………………………13分
(1)根据但单调性的定义法,设变量,作差,变形定号,下结论。
(2)在第一问的基础上,结合单调性,得到函数的最值,然后分析得到参数的范围。
解: (1)证明:设
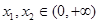 ,且
,且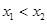
则
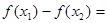
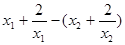 =
=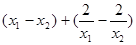 =
=
=
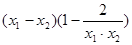 =
=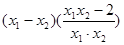 .………4分
.………4分(ⅰ)若
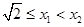 ,
,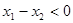 且
且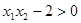 ,
,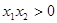 ,所以
,所以 ,
,即
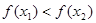 .所以函数
.所以函数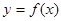 在区间[
在区间[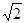 ,+∞)上单调递增.………6分
,+∞)上单调递增.………6分 (ⅱ)若
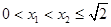 ,则
,则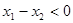 且
且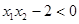 ,
,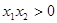 ,
,所以
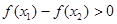 ,即
,即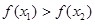 .所以函数
.所以函数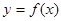 在区间[
在区间[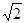 ,+∞)上单调递减.………………………………8分
,+∞)上单调递减.………………………………8分(2)由(1)知函数
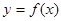 在区间(1,
在区间(1,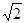 )上单调递减,在区间[
)上单调递减,在区间[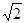 ,2]上单调递增
,2]上单调递增所以
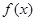 的最小值=
的最小值= ,
,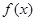 的最大值=
的最大值=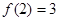 ……………………10分
……………………10分故当
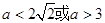 时,方程无解;当
时,方程无解;当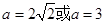 方程有一个解;当
方程有一个解;当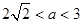 时,方程有两个解.………………………………………13分
时,方程有两个解.………………………………………13分
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
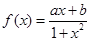 是定义域为
是定义域为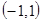 上的奇函数,且
上的奇函数,且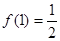
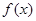 的解析式,
的解析式, 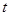 满足
满足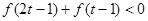 ,求实数
,求实数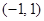 上的函数
上的函数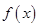 满足:
满足: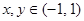 ,都有
,都有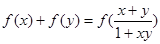
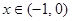 时,有
时,有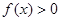 ,求证:(Ⅰ)
,求证:(Ⅰ)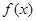 是奇函数;
是奇函数;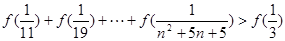
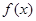 在区间
在区间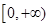 单调增加,则满足
单调增加,则满足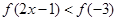 的
的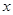 取值范围是
取值范围是 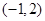
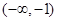
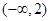
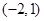
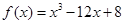 在区间
在区间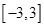 上的最大值与最小值分别为
上的最大值与最小值分别为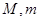 ,则
,则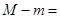 _____________
_____________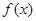 ,满足
,满足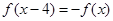 ,且在
,且在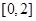 上是增函数,则
上是增函数,则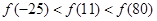
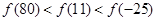
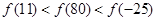
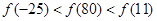
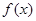 的定义域为R,当
的定义域为R,当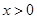 时,
时,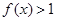 ,且对任意
,且对任意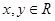 ,都有
,都有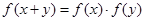 ,且
,且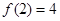 。
。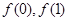 的值;
的值;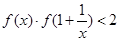 成立,求
成立,求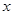 的取值范围。
的取值范围。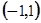 的函数
的函数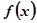
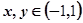 都有
都有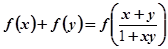 ;
;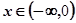 时,
时,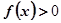 ,回答下列问题:
,回答下列问题: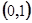 的单调性,并说明理由;
的单调性,并说明理由;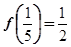 ,求
,求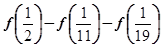 的值.
的值. 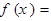
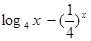 、
、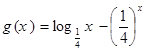 的零点分别为
的零点分别为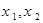 ,则( )
,则( )