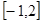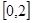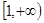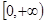题目内容
(本题满分14分)
定义在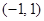 上的函数
上的函数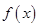 满足:
满足:
(1)对任意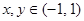 ,都有
,都有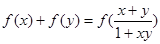
(2)当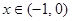 时,有
时,有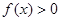 ,求证:(Ⅰ)
,求证:(Ⅰ)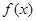 是奇函数;
是奇函数;
(Ⅱ)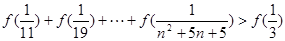
定义在
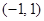 上的函数
上的函数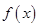 满足:
满足:(1)对任意
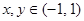 ,都有
,都有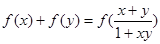
(2)当
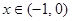 时,有
时,有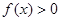 ,求证:(Ⅰ)
,求证:(Ⅰ)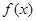 是奇函数;
是奇函数;(Ⅱ)
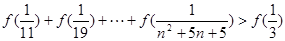
(1) 见解析;(2)见解析。
(1)令y=-x,则f(x)+(-x)=f(0),然后再令x=y=0,从而可求出f(0)=0,因而可判断f(x)是奇函数.
(II)解本小题的关键是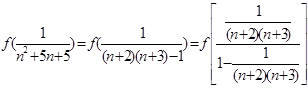
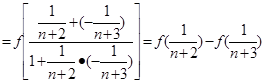 ,然后再叠加求和即可求值.
,然后再叠加求和即可求值.
(1) 令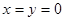 ,则
,则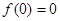 ,再令
,再令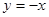 则
则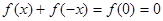
所以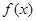 是奇函数. ………………5分
是奇函数. ………………5分
(2)
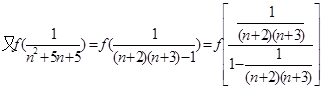

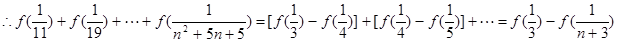
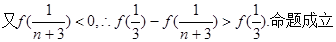 ………………14分
………………14分
(II)解本小题的关键是
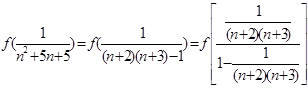
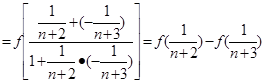 ,然后再叠加求和即可求值.
,然后再叠加求和即可求值.(1) 令
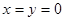 ,则
,则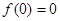 ,再令
,再令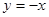 则
则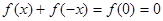
所以
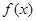 是奇函数. ………………5分
是奇函数. ………………5分(2)
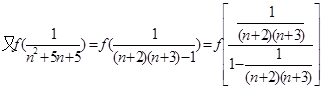

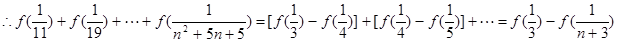
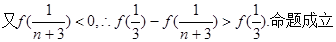 ………………14分
………………14分
练习册系列答案
相关题目
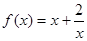 在
在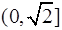 上是减函数,在[
上是减函数,在[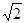 ,+∞)上是增函数;
,+∞)上是增函数;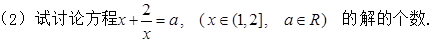
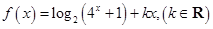 是偶函数.
是偶函数.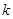 的值;
的值;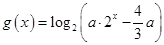 ,其中
,其中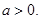 若函数
若函数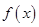 与
与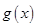 的图象有且只有一个交点,求
的图象有且只有一个交点,求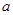 的取值范围.
的取值范围.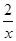 ;④f(x)=
;④f(x)=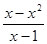 .
.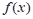 定义在(-1, 1)上,且对任意的
定义在(-1, 1)上,且对任意的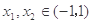
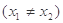 ,都有
,都有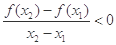 成立,若
成立,若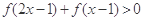 ,则
,则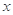 的取值范围是( )
的取值范围是( )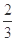 ,1)
,1)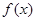 的定义域为
的定义域为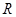 ,当
,当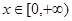 时
时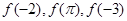 的大小关系是( )
的大小关系是( ) 
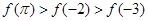
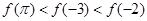
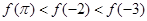
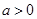 且
且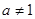 ,
,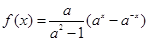
 的奇偶性;
的奇偶性;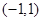 时,求使
时,求使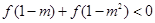 成立的实数
成立的实数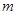 的取值范围.
的取值范围. 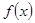 在
在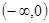 上单调递减,且
上单调递减,且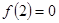 ,则不等式
,则不等式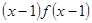 >0的解集是( )
>0的解集是( )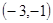
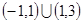
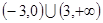
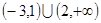
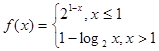 ,则满足
,则满足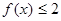 的
的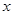 的取值范围是( )
的取值范围是( )