题目内容
定义在R上的奇函数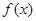 ,满足
,满足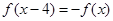 ,且在
,且在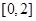 上是增函数,则
上是增函数,则
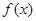 ,满足
,满足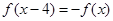 ,且在
,且在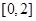 上是增函数,则
上是增函数,则A.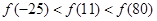 | B.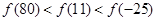 |
C.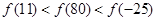 | D.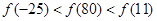 |
D
解:∵f(x)满足f(x-4)=-f(x),∴f(x-8)=f(x),
∴函数是以8为周期的周期函数,则f(-25)=f(-1),f(80)=f(0),f(11)=f(3),
又∵f(x)在R上是奇函数,f(0)=0,得f(80)=f(0)=0,f(-25)=f(-1),
而由f(x-4)=-f(x)得f(11)=f(3)=-f(-1)=f(1),又∵f(x)在区间[0,2]上是增函数,f(x)在R上是奇函数∴f(x)在区间[-2,2]上是增函数
∴f(1)>f(0)>f(-1),即f(-25)<f(80)<f(11),故选D
∴函数是以8为周期的周期函数,则f(-25)=f(-1),f(80)=f(0),f(11)=f(3),
又∵f(x)在R上是奇函数,f(0)=0,得f(80)=f(0)=0,f(-25)=f(-1),
而由f(x-4)=-f(x)得f(11)=f(3)=-f(-1)=f(1),又∵f(x)在区间[0,2]上是增函数,f(x)在R上是奇函数∴f(x)在区间[-2,2]上是增函数
∴f(1)>f(0)>f(-1),即f(-25)<f(80)<f(11),故选D

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
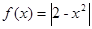 ,若
,若 ,且
,且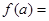
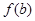 ,则
,则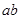 的取值范围是
的取值范围是 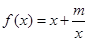 ,且
,且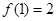
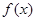 的奇偶性,并证明;
的奇偶性,并证明;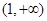 上的单调性,并证明;
上的单调性,并证明;
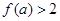 ,求
,求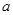 的取值范围。
的取值范围。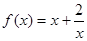 在
在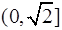 上是减函数,在[
上是减函数,在[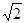 ,+∞)上是增函数;
,+∞)上是增函数;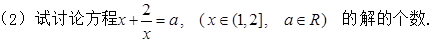
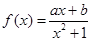 是定义在
是定义在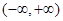 上的奇函数,且
上的奇函数,且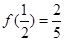 .
.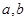 的值.(2)用定义证明
的值.(2)用定义证明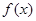 在
在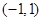 上是增函数;
上是增函数;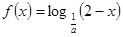 在其定义域上单调递减,则函数
在其定义域上单调递减,则函数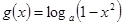 的单调增区间是
的单调增区间是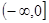
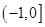
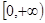
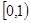
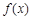 是定义在
是定义在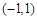 上的减函数,且
上的减函数,且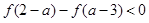 .
. 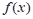 定义在(-1, 1)上,且对任意的
定义在(-1, 1)上,且对任意的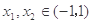
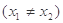 ,都有
,都有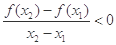 成立,若
成立,若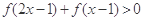 ,则
,则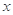 的取值范围是( )
的取值范围是( )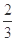 ,1)
,1)