题目内容
(本小题满分12分)设函数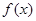 的定义域为R,当
的定义域为R,当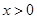 时,
时,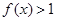 ,且对任意
,且对任意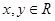 ,都有
,都有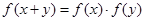 ,且
,且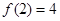 。
。
(1)求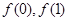 的值;
的值;
(2)证明: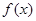 在R上为单调递增函数;
在R上为单调递增函数;
(3)若有不等式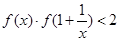 成立,求
成立,求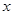 的取值范围。
的取值范围。
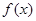 的定义域为R,当
的定义域为R,当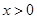 时,
时,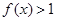 ,且对任意
,且对任意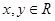 ,都有
,都有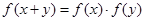 ,且
,且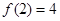 。
。(1)求
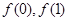 的值;
的值;(2)证明:
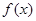 在R上为单调递增函数;
在R上为单调递增函数;(3)若有不等式
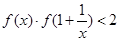 成立,求
成立,求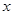 的取值范围。
的取值范围。(1) ,
,  ;(2)
;(2)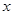 的取值范围是
的取值范围是 。
。
 ,
,  ;(2)
;(2)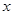 的取值范围是
的取值范围是 。
。本题主要考查了抽象函数表达式反映函数性质及抽象函数表达式的应用,函数单调性的定义及其证明,利用函数性质和函数的单调性解不等式的方法,转化化归的思想方法。
(1)利用赋值法,令x=2,y=0即可求得f(0)的值,令x=y=1,即可求得f(1)的值;
(2)先证明0<f(x)<1,再利用函数单调性的定义,设任意的x1,x2∈R,且x1<x2,利用抽象表达式和已知函数性质证明f(x1)<f(x2),即可得证;
(3)利用抽象表达式,先将不等式化为f(x+1+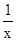 )<f(1),再利用函数的单调性将不等式转化为分式不等式即可得解集。
)<f(1),再利用函数的单调性将不等式转化为分式不等式即可得解集。
解(1)因为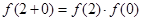 ,所以
,所以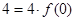 ,所以
,所以 ,又因为
,又因为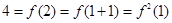 ,且当
,且当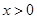 时,
时,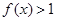 ,所以
,所以
(2)当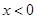 时,
时,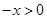 ,所以
,所以 ,而
,而 ,所以
,所以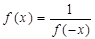 ,所以
,所以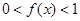 ,对任意的
,对任意的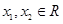 ,当
,当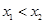 时,有
时,有


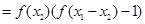 ,因为
,因为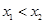 ,所以
,所以 ,所以
,所以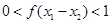 ,即
,即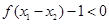 ,所以
,所以 ,即
,即 ,所以
,所以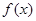 在R上是单调递增函数(3)因为
在R上是单调递增函数(3)因为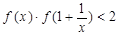 ,所以
,所以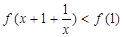 ,而
,而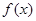 在R上是单调递增函数,所以
在R上是单调递增函数,所以 ,即:
,即: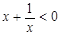 ,所以
,所以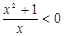 ,所以
,所以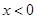 ,所以
,所以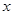 的取值范围是
的取值范围是
(1)利用赋值法,令x=2,y=0即可求得f(0)的值,令x=y=1,即可求得f(1)的值;
(2)先证明0<f(x)<1,再利用函数单调性的定义,设任意的x1,x2∈R,且x1<x2,利用抽象表达式和已知函数性质证明f(x1)<f(x2),即可得证;
(3)利用抽象表达式,先将不等式化为f(x+1+
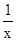 )<f(1),再利用函数的单调性将不等式转化为分式不等式即可得解集。
)<f(1),再利用函数的单调性将不等式转化为分式不等式即可得解集。解(1)因为
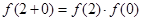 ,所以
,所以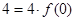 ,所以
,所以 ,又因为
,又因为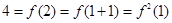 ,且当
,且当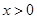 时,
时,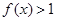 ,所以
,所以
(2)当
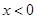 时,
时,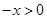 ,所以
,所以 ,而
,而 ,所以
,所以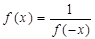 ,所以
,所以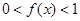 ,对任意的
,对任意的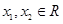 ,当
,当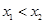 时,有
时,有

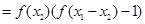 ,因为
,因为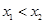 ,所以
,所以 ,所以
,所以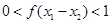 ,即
,即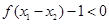 ,所以
,所以 ,即
,即 ,所以
,所以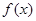 在R上是单调递增函数(3)因为
在R上是单调递增函数(3)因为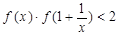 ,所以
,所以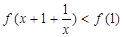 ,而
,而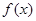 在R上是单调递增函数,所以
在R上是单调递增函数,所以 ,即:
,即: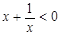 ,所以
,所以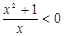 ,所以
,所以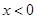 ,所以
,所以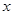 的取值范围是
的取值范围是

练习册系列答案
相关题目
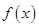 是定义在
是定义在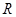 上单调函数,对任意实数
上单调函数,对任意实数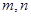 有:
有: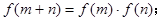 且
且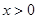 时,
时,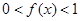 .
.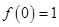 ;
;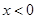 时,
时,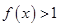 ;
;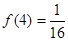 时,求使
时,求使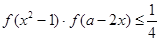 对任意实数
对任意实数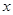 恒成立的参数
恒成立的参数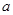 的取值范围.
的取值范围.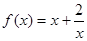 在
在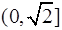 上是减函数,在[
上是减函数,在[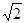 ,+∞)上是增函数;
,+∞)上是增函数;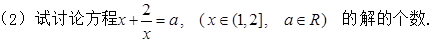
 ,则满足不等式
,则满足不等式 的
的 的取值范围
的取值范围



 在
在 上是增函数,且最小值是1,则它在
上是增函数,且最小值是1,则它在 上是( )
上是( )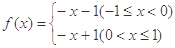 ,则
,则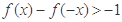 的解集为( )
的解集为( ) )∪(0,1]
)∪(0,1]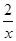 ;④f(x)=
;④f(x)=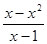 .
.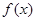 的定义域为
的定义域为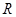 ,当
,当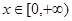 时
时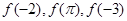 的大小关系是( )
的大小关系是( ) 
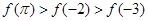
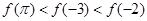
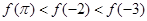
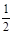 )
)