题目内容
f（n）=cos(
+
)，则f（1）+f（2）+f（3）+…+f（2012）=______．
| 2nπ |
| 2 |
| π |
| 4 |
∵f（n）=cos（
+
）=cos（nπ+
），
∴f（1）+f（2）=cos（π+
）+cos（2π+
）=0，
同理可得，f（3）+f（4）=…=f（2011）+f（2012）=0，
∴f（1）+f（2）+f（3）+…+f（2012）=0．
故答案为：0
| 2nπ |
| 2 |
| π |
| 4 |
| π |
| 4 |
∴f（1）+f（2）=cos（π+
| π |
| 4 |
| π |
| 4 |
同理可得，f（3）+f（4）=…=f（2011）+f（2012）=0，
∴f（1）+f（2）+f（3）+…+f（2012）=0．
故答案为：0
练习册系列答案
相关题目
（n∈N*），则f（1）+f（2）+f（3）+…+f（100）=________．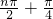
），则f（1）+f（2）+…+f（2006）=________．
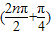，则f（1）+f（2）+f（3）+…+f（2012）= ．