题目内容
已知f(n)=cos (n∈N*),则f(1)+f(2)+f(3)+…+f(100)=________.
(n∈N*),则f(1)+f(2)+f(3)+…+f(100)=________.
解:当n-1时,f(1)=cos =
= ,当n=2时,f(2)=cos
,当n=2时,f(2)=cos ,当n=3时,
,当n=3时, ,当n=4时,
,当n=4时, ,
,
当n=5时,f(5)= ,当n=6时,f(6)=
,当n=6时,f(6)= ,当n=7时,f(7)=
,当n=7时,f(7)= ,
,
当n=8时,f(8)= ,当n=9时,f(9)=
,当n=9时,f(9)=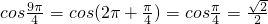 ,…由以上数值出现的规律可以知道,此函数的一个周期为T=8,
,…由以上数值出现的规律可以知道,此函数的一个周期为T=8,
利用函数的周期性,而f(1)+f(2)+f(3)+…f(8)=0,则f(1)+f(2)+f(3)+…+f(100)=f(1)+F(2)+f(3)+f(4)= =-1.
=-1.
故答案为:-1.
分析:由已知f(n)=cos (n∈N*)的解析式可以知道该函数是周期函数,所以可以先取一些函数值找起规律即可.
(n∈N*)的解析式可以知道该函数是周期函数,所以可以先取一些函数值找起规律即可.
点评:此题考查了求函数解析式求函数值,并利用观察法得到函数的周期,利用函数的周期性进行对于很多项函数值的求解.
 =
= ,当n=2时,f(2)=cos
,当n=2时,f(2)=cos ,当n=3时,
,当n=3时, ,当n=4时,
,当n=4时, ,
,当n=5时,f(5)=
 ,当n=6时,f(6)=
,当n=6时,f(6)= ,当n=7时,f(7)=
,当n=7时,f(7)= ,
,当n=8时,f(8)=
 ,当n=9时,f(9)=
,当n=9时,f(9)=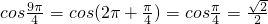 ,…由以上数值出现的规律可以知道,此函数的一个周期为T=8,
,…由以上数值出现的规律可以知道,此函数的一个周期为T=8,利用函数的周期性,而f(1)+f(2)+f(3)+…f(8)=0,则f(1)+f(2)+f(3)+…+f(100)=f(1)+F(2)+f(3)+f(4)=
 =-1.
=-1.故答案为:-1.
分析:由已知f(n)=cos
 (n∈N*)的解析式可以知道该函数是周期函数,所以可以先取一些函数值找起规律即可.
(n∈N*)的解析式可以知道该函数是周期函数,所以可以先取一些函数值找起规律即可.点评:此题考查了求函数解析式求函数值,并利用观察法得到函数的周期,利用函数的周期性进行对于很多项函数值的求解.

练习册系列答案
相关题目
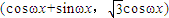 ,n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m•n,且f(x)的对称中心到f(x)对称轴的最近距离不小于
,n=(cosωx-sinωx,2sinωx),其中ω>0,若函数f(x)=m•n,且f(x)的对称中心到f(x)对称轴的最近距离不小于