题目内容
f（n）=cos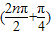
，则f（1）+f（2）+f（3）+…+f（2012）= ．
【答案】分析：由f（n）=cos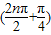
=cos（nπ+
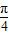），可求得f（1）+f（2）=f（3）+f（4）=…=f（2011）+f（2012）=0，从而可求得答案．
解答：解：∵f（n）=cos（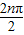
+
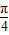）=cos（nπ+
），
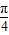∴f（1）+f（2）=cos（π+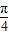
）+cos（2π+
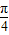）=0，
同理可得，f（3）+f（4）=…=f（2011）+f（2012）=0，
∴f（1）+f（2）+f（3）+…+f（2012）=0．
故答案为：0
点评：本题考查三角函数的周期性及其求法，求得f（1）+f（2）=f（3）+f（4）=…=f（2011）+f（2012）=0是关键，属于基础题．
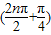=cos（nπ+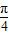），可求得f（1）+f（2）=f（3）+f（4）=…=f（2011）+f（2012）=0，从而可求得答案．解答：解：∵f（n）=cos（
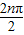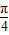+）=cos（nπ+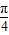），∴f（1）+f（2）=cos（π+
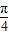）+cos（2π+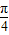）=0，同理可得，f（3）+f（4）=…=f（2011）+f（2012）=0，
∴f（1）+f（2）+f（3）+…+f（2012）=0．
故答案为：0
点评：本题考查三角函数的周期性及其求法，求得f（1）+f（2）=f（3）+f（4）=…=f（2011）+f（2012）=0是关键，属于基础题．
练习册系列答案
相关题目
（n∈N*），则f（1）+f（2）+f（3）+…+f（100）=________．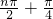
），则f（1）+f（2）+…+f（2006）=________．