题目内容
13.(1)设函数f(x)=2x+3,g(x+2)=f(x),求g(x)的表达式.(2)已知f(x)是定义在R上的奇函数,当x>0时,f(x)=-$\sqrt{x}$(1+x),求f(x)的解析式.
分析 (1)令x+2=t,则x=t-2,可得g(t)=f(t-2),即可得出.
(2)利用函数的奇偶性即可得出.
解答 解:(1)令x+2=t,则x=t-2,∴g(t)=f(t-2)=2(t-2)+3=2t-1,
把t换成x可得:g(x)=2x-1.
(2)设x<0,则-x>0,
∵当x>0时,f(x)=-$\sqrt{x}$(1+x),
∴f(-x)=-$\sqrt{-x}$(1-x),
又f(x)是定义在R上的奇函数,
∴f(0)=0,f(x)=-f(-x)=$\sqrt{-x}$(1-x).
∴f(x)=$\left\{\begin{array}{l}{-\sqrt{x}(1+x),x≥0}\\{\sqrt{-x}(1-x),x<0}\end{array}\right.$.
点评 本题考查了函数的奇偶性、“换元法”求函数的解析式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.已知函数f(x)=ax+7,f(-3)=5,则f(3)的值为( )
| A. | 9 | B. | -9 | C. | -5 | D. | 7 |
5.在等差数列{an}中,已知a5+a7=8,则该数列前11项和S11=( )
| A. | 44 | B. | 55 | C. | 143 | D. | 176 |
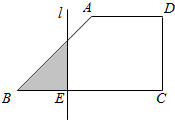 如图,底角∠ABE=45°的直角梯形ABCD,底边BC长为4cm,腰长AB为$2\sqrt{2}$cm,当一条垂直于底边BC的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BE=x,试写出阴影部分的面积y与x的函数关系式,并画出函数大致图象.
如图,底角∠ABE=45°的直角梯形ABCD,底边BC长为4cm,腰长AB为$2\sqrt{2}$cm,当一条垂直于底边BC的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BE=x,试写出阴影部分的面积y与x的函数关系式,并画出函数大致图象.