题目内容

1．已知函数f（x）=ax+7，f（-3）=5，则f（3）的值为（　　）
A．9B．-9C．-5D．7

分析 利用函数的解析式求出a，然后求解函数值即可．

解答 解：函数f（x）=ax+7，f（-3）=5，
可得-3a+7=5，解得a=$\frac{2}{3}$，
函数的解析式为：f（x）=$\frac{2}{3}$x+7
f（3）=$\frac{2}{3}×3+7=9$．
故选：A．

点评 本题考查函数的解析式的求法，函数值的求法，考查计算能力．

练习册系列答案
相关题目
8．已知直线l1：（2a+b）x+（a+b）y+a-b=0与直线l2：m2x+2y-2n2=0恒有一个公共点，则m+n的最大值为$\sqrt{6}$．
12．已知f（x）=ax2+2x在[2，4]上单调，则a的取值范围是a≤-$\frac{1}{2}$或a≥-$\frac{1}{4}$．
9．在复平面内，复数z=i（1+2i）的共轭复数（　　）
A．2-iB．-2-iC．2+iD．-2+i
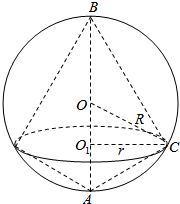16． 已知两个圆锥有公共底面，且两圆锥的顶点和底面的圆周都在同一个球面上．若圆锥底面面积是这个球面面积的$\frac{3}{16}$，求这两个圆锥中，体积较小者与体积较大者的高的比值．
6．下列结论正确的是（2）（3）．
（1）函数f（x）=sinx在第一象限是增函数；
（2）△ABC中，“A＞B”是“cosA＜cosB”的充要条件；
（3）设$\overrightarrow{a}$，$\overrightarrow{b}$是非零向量，命题“若|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|，则?t∈R，使得$\overrightarrow{a}$=t$\overrightarrow{b}$”的否命题和逆否命题都是真命题；
（4）函数f（x）=2x3-3x2，x∈[-2，t]（-2＜t＜1）的最大值为0．
13．（1）设函数f（x）=2x+3，g（x+2）=f（x），求g（x）的表达式．
（2）已知f（x）是定义在R上的奇函数，当x＞0时，f（x）=-$\sqrt{x}$（1+x），求f（x）的解析式．
10．定义在R上的偶函数f（x）在[0，+∞）内单调递减，则下列判断正确的是（　　）
A．f（2a）＜f（-a）B．f（π）＞f（-3）C．$f（-\frac{{\sqrt{3}}}{2}）＜f（\frac{4}{5}）$D．f（a2+1）＜f（1）
11．已知函数f（x）=lnx+$\frac{a-x}{x}$，其中a为常数，且a＞0．
（1）若曲线y=f（x）在点（1，f（1））处的切线与直线y=$\frac{1}{2}$x+1垂直，求a的值；
（2）求函数f（x）在区间[1，2]上的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网