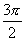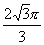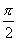题目内容
.如图所示,已知正四棱锥S—ABCD中,底面边长为a,侧棱长为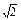 a.
a.
(1)求它的外接球的体积;
(2)求它的内切球的表面积.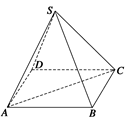
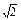 a.
a.(1)求它的外接球的体积;
(2)求它的内切球的表面积.

(1)V球=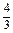
 R3=
R3=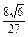
 a3(2)V棱锥=
a3(2)V棱锥=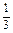 S底h=
S底h=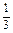 a2×
a2× a=
a=
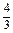
 R3=
R3=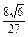
 a3(2)V棱锥=
a3(2)V棱锥=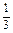 S底h=
S底h=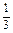 a2×
a2× a=
a=
(1)设外接球的半径为R,球心为O,则OA=OC=OS,所以O为△SAC的外心,
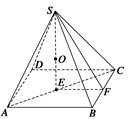
即△SAC的外接圆半径就是球的半径.
∵AB=BC=a,∴AC=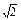 a.
a.
∵SA=SC=AC=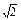 a,∴△SAC为正三角形.
a,∴△SAC为正三角形.
由正弦定理得2R= ,
,
因此,R=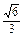 a,V球=
a,V球=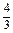
 R3=
R3=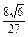
 a3.
a3.
(2)设内切球半径为r,作SE⊥底面ABCD于E,
作SF⊥BC于F,连接EF,
则有SF=
=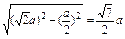 .
.
S△SBC= BC·SF=
BC·SF= a×
a×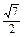 a=
a=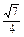 a2.
a2.
S棱锥全=4S△SBC+S底=(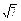 +1)a2.
+1)a2.
又SE=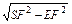 =
=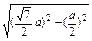 =
=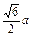 ,
,
∴V棱锥=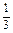 S底h=
S底h=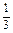 a2×
a2× a=
a= .
.
∴r=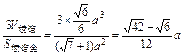 ,
,
S球=4 r2=
r2=
 a2.
a2.

即△SAC的外接圆半径就是球的半径.
∵AB=BC=a,∴AC=
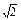 a.
a.∵SA=SC=AC=
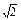 a,∴△SAC为正三角形.
a,∴△SAC为正三角形.由正弦定理得2R=
 ,
,因此,R=
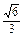 a,V球=
a,V球=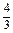
 R3=
R3=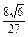
 a3.
a3.(2)设内切球半径为r,作SE⊥底面ABCD于E,
作SF⊥BC于F,连接EF,
则有SF=

=
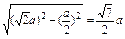 .
.S△SBC=
 BC·SF=
BC·SF= a×
a×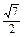 a=
a=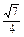 a2.
a2.S棱锥全=4S△SBC+S底=(
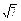 +1)a2.
+1)a2.又SE=
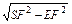 =
=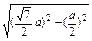 =
=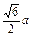 ,
,∴V棱锥=
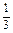 S底h=
S底h=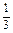 a2×
a2× a=
a= .
.∴r=
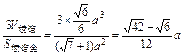 ,
,S球=4
 r2=
r2=
 a2.
a2.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 cm2
cm2 cm2
cm2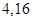 ,高为
,高为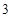 ,则该棱台的体积为( ).
,则该棱台的体积为( ).
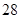

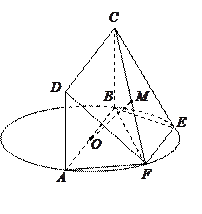


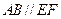

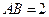

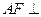 平面
平面 ;
;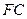 的中点为
的中点为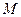 ,求证:
,求证: 平面
平面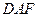 ;
; 的体积.
的体积.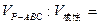 __________
__________