已知等差数列{an}的公差为2.若a4是a2.a8的等比中项.则数列{an}的前5项和为S5=30．题目和参考答案——青夏教育精英家教网——

题目内容

3．已知等差数列{a_n}的公差为2，若a₄是a₂，a₈的等比中项，则数列{a_n}的前5项和为S₅=30．

分析 a₄是a₂，a₈的等比中项，可得${a}_{4}^{2}={a}_{2}•{a}_{8}$，再利用等差数列的通项公式及其前n项和公式即可得出．

解答解：∵a₄是a₂，a₈的等比中项，
∴${a}_{4}^{2}={a}_{2}•{a}_{8}$，
∴$（{a}_{1}+3×2）^{2}$=（a₁+2）（a₁+7×2），
化为a₁=2，
∴S₅=$5×2+\frac{5×4}{2}×2$=30．
故答案为：30．

点评本题考查了等差数列与等比数列的通项公式及其前n项和公式，属于基础题．

练习册系列答案

练习册人民教育出版社系列答案

课堂内外练测步步高系列答案

新目标检测同步单元测试卷系列答案

夺冠计划创新测评系列答案

概念地图系列答案

练习部分系列答案

课时测评导学导思导练系列答案

100分冲刺卷系列答案

初中单元期末卷系列答案

创新测试卷期末直通车系列答案

相关题目

14．3对夫妇去看电影，6个人坐成一排，若女性的邻座只能是其丈夫或其他女性，则坐法的种数为（　　）

14．已知M（x₀，y₀）是抛物线C：y²=8x上一点，F为抛物线C的焦点，若|MF|＞4，则x₀的取值范围是（　　）

11．已知向量$\overrightarrow{a}$=（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），$\overrightarrow{b}$=（2cosθ，2sinθ），0＜θ＜π．
（1）若$\overrightarrow{a}$∥$\overrightarrow{b}$，求角θ的大小；
（2）若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{b}$|，求sinθ的值．

18．数列{a_n}满足a₁=1，且对于任意的n∈N^*都有a_n+1=a₁+a_n+n，则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{2015}}}}$等于（　　）

$\frac{4028}{2015}$

$\frac{2014}{2015}$

$\frac{4030}{2016}$

$\frac{2015}{2016}$

8．已知全集U=R，集合A={x|-1≤x≤1}，B={x|x²-2x≥0}，则A∩B=[-1，0]，A∪（∁_UB）=[-1.2）．

15．sin15°-cos15°=（　　）

$\frac{\sqrt{2}}{2}$

-$\frac{\sqrt{2}}{2}$

12．已知点A（0，1），直线l：y=kx+m与圆O：x²+y²=1交于B，C两点，△ABC与△OBC的面积分别为S₁，S₂，若S₁≥2S₂，且∠BAC=60°，则m的取值范围是[-1，-$\frac{1}{2}$]．

将函数的图象向右平移个单位后得到函数的图象，若函数在区间和上均单调递增，则实数的取值范围是（）

A． B．

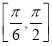
C． D．