题目内容
(1)已知△ABC的顶点A(1,1),B(3,2),C(2,4),求△ABC的面积.
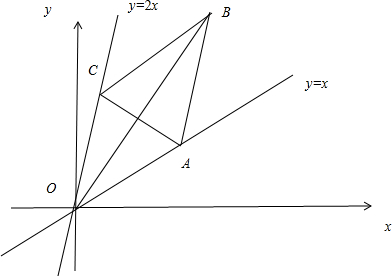
(2)若△ABC的顶点A在直线y=x上运动,顶点B(6,8),顶点C在线段y=2x (3≤x≤5)上运动,且A、C、B三点的横坐标成等差数列,问△ABC的面积是否存在最大值?若存在求出最大值,若不存在,说明理由.
(2)若△ABC的顶点A在直线y=x上运动,顶点B(6,8),顶点C在线段y=2x (3≤x≤5)上运动,且A、C、B三点的横坐标成等差数列,问△ABC的面积是否存在最大值?若存在求出最大值,若不存在,说明理由.
分析:(1)由两点间的距离公式可得,AB=
,BC=
,AC=
,可求三角形的面积
(2)由题意可设A(a,a),C(b,2b)(3≤b≤5),由A、C、B三点的横坐标成等差数列可得2b=a+6及3≤b≤5可得0≤a≤4,C(
,a+6),而S△ABC=S△OAB+S△OBC-S△OAC=-
(a2-2a-24)=-
(a-1)2+
,结合二次函数的性质可求面积的最大值
| 5 |
| 5 |
| 10 |
(2)由题意可设A(a,a),C(b,2b)(3≤b≤5),由A、C、B三点的横坐标成等差数列可得2b=a+6及3≤b≤5可得0≤a≤4,C(
| a+6 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 25 |
| 4 |
解答:解:(1)由两点间的距离公式可得,AB=
,BC=
,AC=
∴AB2+BC2=AC2即AB⊥BC
S△ABC=
AB•BC=
×
×
=
(2)由题意可设A(a,a),C(b,2b)(3≤b≤5)
A、C、B三点的横坐标成等差数列可得2b=a+6
∴b=
且由3≤b≤5可得0≤a≤4即C(
,a+6)
设C,A到直线OB:y=
x的距离分别为h1,h2,点C到直线y=x的距离为h3
则h1=
,h2=
,h3=
S△ABC=S△OAB+S△OBC-S△OAC
=
OB•(h1+h2)-
OA•h3=
×10×
-
×
a×
=-
(a2-2a-24)=-
(a-1)2+
当a=1时,S△ABC的面积最大值
| 5 |
| 5 |
| 10 |
∴AB2+BC2=AC2即AB⊥BC
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
(2)由题意可设A(a,a),C(b,2b)(3≤b≤5)
A、C、B三点的横坐标成等差数列可得2b=a+6
∴b=
| a+6 |
| 2 |
| a+6 |
| 2 |
设C,A到直线OB:y=
| 4 |
| 3 |
则h1=
| a+6 |
| 5 |
| a |
| 5 |
| a+6 | ||
2
|
S△ABC=S△OAB+S△OBC-S△OAC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2a+6 |
| 5 |
| 1 |
| 2 |
| 2 |
| a+6 | ||
2
|
=-
| 1 |
| 4 |
| 1 |
| 4 |
| 25 |
| 4 |
当a=1时,S△ABC的面积最大值
| 25 |
| 4 |

点评:本题主要考查了三角形的面积公式的应用,等差数列的性质的应用,解题(2)的关键是要准确表示出三角形的面积,结合二次函数的性质进行求解,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 内一点M(2,1)引一条弦,使得弦被M点平分,求此弦所在的直线方程.
内一点M(2,1)引一条弦,使得弦被M点平分,求此弦所在的直线方程.