Question

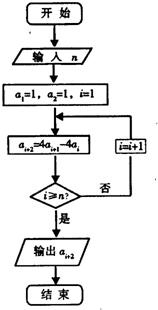已知数列{a_n}满足如图所示的程序框图．
（I）写出数列{a_n}的一个递推关系式；
（II）证明：{a_n+1-2a_n}是等比数列；
（III）证明{

an

2n

}是等差数列，并求{a_n}的通项公式．

Answer 1

分析：（I） 由程序框图可直接得到a _n+2=4 a_n+1-4a_n
（Ⅱ）将a _n+2=4 a_n+1-4a_n移向变形得出a_n+1-2a_n =2（a _n+1-2a_n），从而可证{a_n+1-2a_n}是等比数列；
（Ⅲ）由（Ⅱ）可求出a_n+1-2a_n=-2 ^n-1 两边同除以2ⁿ⁺¹变形构造出

an+1

2n+1

-

an

2n

=

1

4

，从而可解决．

解答：解：（I） 由程序框图可知，数列{an}的一个递推关系式
a₁=1，a₂=1，a _n+2=4 a_n+1-4a_n
（II）由a_n+1-2a_n =2（a _n+1-2a_n），且a₂-2a₁=-1
∴数列{a_n+1-2a_n}是以-1为首项，2为公比的等比数列
（III） 由（II）有a_n+1-2a_n=-2 ^n-1
∴

an+1

2n+1

-

an

2n

⁼

1

4

^，又

a2

21

⁼

1

2

^∴_l数列{

an

2n

}是以

1

2

为首项，以-

1

4

为公差的等差数列
∴

an

2n

=

1

2

+ (-

1

4

)(n-1)，
∴a_n=(

3-n

4

)•2n

点评：本题考查程序框图知识，等差数列、等比数列的定义及判定．考查转化、计算、分析解决问题的能力．