Question

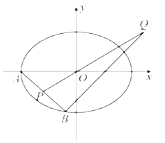
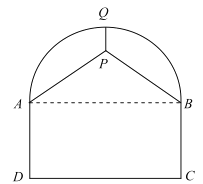
【题目】已知质点P绕点M逆时针做匀速圆周运动（如图1），质点P相对于水平直线l的位置用y（米）表示，质点在l上方时，y为正，反之，y为负，是质点与直线l的距离，位置y与时间t（秒）之间的关系为（其中，，）其图象如图2所示.

（1）写出质点P运动的圆形轨道半径及从初始位置到最高点所需要的时间；

（2）求的解析式，并指出质点P第二次出现在直线l上的时刻.

Answer 1

【答案】（1），秒（2）；质点P第二次出现在直线l上的时刻为

【解析】

（1）圆形轨道半径就是函数的振幅，进而求得从初始位置到最高点所需要的时间；

（2）结合函数的图象，求得函数的解析式，令，即可求解质点P第二次出现在直线l上的时刻.

（1）由题意，可得圆形轨道半径就是函数的振幅，

从初始位置到最高点所需要的时间为秒.

（2）当时，可得，即，即，

又因为，可得，所以，

又函数图象过，可得，即，

解得，，

取，得，所以，

令，则，即，解得秒，

所以质点P第二次出现在直线l上的时刻为