题目内容
已知函数f(x)=![]() ax2-(2a+1)x+2lnx(a∈R).
ax2-(2a+1)x+2lnx(a∈R).
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)求f(x)的单调区间;
(3)设g(x)=x2-2x,若对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),求a的取值范围.
解析 f′(x)=ax-(2a+1)+![]() (x>0).
(x>0).
(1)由f′(1)=f′(3),解得a=![]() .
.
(2)f′(x)=![]() (x>0).
(x>0).
①当a≤0时,x>0,ax-1<0,
在区间(0,2)上f′(x)>0;在区间(2,+∞)上f′(x)<0.
故f(x)的单调递增区间(0,2),单调递减区间是(2,+∞).
②当0<a<![]() 时,
时,![]() >2,
>2,
在区间(0,2)和![]() 上f′(x)>0;在区间
上f′(x)>0;在区间![]() 上f′(x)<0,故f(x)的单调递增区间是(0,2)和(
上f′(x)<0,故f(x)的单调递增区间是(0,2)和(![]() ,+∞),
,+∞),
单调递减区间是![]() .
.
③当a=![]() 时,f′(x)=
时,f′(x)=![]() ,
,
故f(x)的单调递增区间是(0,+∞).
④当a>![]() 时,0<
时,0<![]() <2,
<2,
在区间![]() 和(2,+∞)上f′(x)>0;在区间
和(2,+∞)上f′(x)>0;在区间![]() 上f′(x)<0
上f′(x)<0![]() ,故f(x)的单调递增区间是
,故f(x)的单调递增区间是![]() 和(2,+∞),单调递减区间是
和(2,+∞),单调递减区间是![]() .
.
(3)由已知,在(0,2]上有f(x)max<g(x)max.
由已知,g(x)max=0,由(2)可知,
①当a≤![]() 时,f(x)在(0,2]上单调递增,
时,f(x)在(0,2]上单调递增,
故f(x)max=f(2)=2a-2(2a+1)+2ln2=-2a-2+2ln2.
所以,-2a-2+2ln2<0,解得a>ln2-1.
故ln2-1<a≤![]() .
.
②当a>![]() 时,f(x)在
时,f(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,故f(x)max=f(
上单调递减,故f(x)max=f(![]() )=-2-
)=-2-![]() -2lna.
-2lna.
由a>![]() 可知lna>ln
可知lna>ln![]() >ln
>ln![]() =-1,2lna>-2,-2lna<2.
=-1,2lna>-2,-2lna<2.
所以,-2-2lna<0,f(x)max<0.
综上所述,a>ln2-1.

练习册系列答案
相关题目
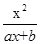 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4. .
. (a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
(a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值. )
)