题目内容
设函数f(x)=2x3-3(a+1)x2+6ax,
(1)当a=1时,试用单调性的定义证明f(x)为单调增函数;
(2)当x∈[1,3]时,f(x)的最小值为4,求a的值.
答案:
解析:
解析:
|
(1)当 故 (2)①当 由于 ②当 |

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
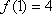 ,即
,即