题目内容
已知F1、F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线交椭圆于A、B两点,若△ABF2是正三角形,则这个椭圆的离心率为( )
A.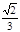 B.
B.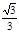 C.
C.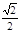 D.
D.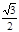
【答案】
B
【解析】解:∵△ABF2是正三角形,∴∠AF2B=60°,∵直线AB与椭圆长轴垂直,
∴F2F1是正三角形△ABF2的高,∠AF2F1=1 2 ×60°=30°,Rt△AF2F1中,设|AF1|=m,sin30°=|AF1| |AF2| =1 2 ,∴|AF2|=2m,|F1F2|2 = |AF2|2-|AF1|2 = 3 m
因此,椭圆的长轴2a=|AF1|+|AF2|=3m,焦距2c= 3 m∴椭圆的离心率为e=c 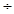 a
=2c
a
=2c 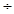 2a
=
2a
=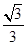 故答案为: B
故答案为: B

练习册系列答案
相关题目