题目内容
2．已知直线l过点（1，0），倾斜角是直线2x-y-2=0的倾斜角的2倍，则直线l的方程为（ ）| A． | 4x-y-4=0 | B． | 4x+y-4=0 | C． | 3x+4y-3=0 | D． | 4x+3y-4=0 |
分析 先求直线x-2y-1=0的斜率，进而转化为倾斜角，用2倍角公式求过点（1，0）的斜率，再求解直线方程．
解答 解：直线x-2y-1=0的斜率为k=0.5，倾斜角为α，所以tanα=0.5，
过点（1，0）的倾斜角为2α，
其斜率为tan2α=$\frac{2tanα}{1-{tan}^{2}α}$=-$\frac{4}{3}$，
故所求直线方程为：y=-$\frac{4}{3}$（x-1），即4x-3y-4=0
故选：D
点评 本题考查的知识点是点斜式方程，二倍角的正切公式，是直线与三角函数的综合应用，难度中档．
练习册系列答案
相关题目
12．世界杯共有32支参赛队伍，则最终冠军、亚军的归属情况的种数为（假设所有队伍均有希望打进决赛）（ ）
| A． | 63 | B． | 64 | C． | 496 | D． | 992 |
13．在（1+x）n的展开式中，只有第4项的系数最大，则n等于（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
10．已知学生的数学成绩与物理成绩具有线性相关关系，某班6名学生的数学和物理成绩如表：
（1）求物理成绩y对数学成绩x的线性回归方程；
（2）当某位学生的数学成绩为70分时，预测他的物理成绩．
参考公式：用最小二乘法求线性回归方程$\widehat{y}=\widehat{b}x+\widehat{a}$的系数公式：
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}=\overline{y}-a\overline{x}$．
参考数据：832+782+732+682+632+732=32224，
83×75+78×65+73×75+68×65+63×60+73×80=30810．
 | A | B | C | D | E | F |
| 数学成绩（x） | 83 | 78 | 73 | 68 | 63 | 73 |
| 物理成绩（y） | 75 | 65 | 75 | 65 | 60 | 80 |
（2）当某位学生的数学成绩为70分时，预测他的物理成绩．
参考公式：用最小二乘法求线性回归方程$\widehat{y}=\widehat{b}x+\widehat{a}$的系数公式：
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}=\overline{y}-a\overline{x}$．
参考数据：832+782+732+682+632+732=32224，
83×75+78×65+73×75+68×65+63×60+73×80=30810．
17．
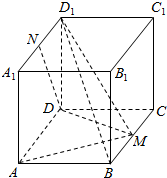已知ABCD-A1B1C1D1是长方体，且AB=AA1=2，AD=4，M是BC中点，N是A1D1中点．
（Ⅰ）求证：AM⊥平面MDD1；
（Ⅱ）求证：DN⊥MD1；
（Ⅲ）求三棱锥A-MBD1的体积．
已知ABCD-A1B1C1D1是长方体，且AB=AA1=2，AD=4，M是BC中点，N是A1D1中点．（Ⅰ）求证：AM⊥平面MDD1；
（Ⅱ）求证：DN⊥MD1；
（Ⅲ）求三棱锥A-MBD1的体积．
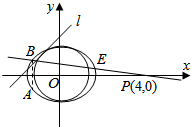如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，以原点为圆心、椭圆的短半径为半径的圆与直线l：x-y+$\sqrt{6}$=0相切．
3．已知等差数列{an}的公差d≠0，且a1，a5，a17依次成等比，则这个等比数列的公比是（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{1}{3}$ | D． | 3 |